练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    对于函数
    （1）探究函数f（x）的单调性，并给予证明；
    （2）是否存在实数a使函数f（x）为奇函数？
    （3）求函数f（x）的值域．
    【答案】分析：（1）利用导数大于0，可得函数f（x）在R上单调增；
    （2）若函数f（x）为奇函数，则f（-x）=-f（x），从而可建立方程，由此可得存在实数a使函数f（x）为奇函数；
    （3）先确定，进而可求函数f（x）的值域．
    解答：解：（1）函数f（x）在R上单调增．
    证明：求导函数可得：
    ∵x∈R，∴
    ∴函数f（x）在R上单调增．
    （2）解：若函数f（x）为奇函数，则f（-x）=-f（x）
    ∴
    ∴2a=1
    ∴
    ∴当时，函数f（x）为奇函数；
    （3）解：∵2x＞0
    ∴2x+1＞1
    ∴
    ∴
    ∴
    ∴函数f（x）的值域为（a-1，a）
    点评：本题综合考查函数的单调性与奇偶性，考查函数的值域，解题的关键是正确理解函数的单调性与奇偶性，掌握求函数值域的一般方法，
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

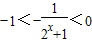
    科目：高中数学 来源： 题型：

    对于函数f(x)=a-
    12x+1
    (a∈R)：
    （1）探究函数f（x）的单调性，并给予证明；
    （2）是否存在实数a使函数f（x）为奇函数？
    （3）求函数f（x）的值域．

    查看答案和解析>>

    科目：高中数学 来源：上海市部分重点中学2010届高三第二次联考数学文科试题 题型：044

    对于定义在D上的函数y＝f(x)，若存在x0∈D，对任意的x∈D，都有f(x)≥f(x0)，则称函数f(x)在区间D上有下界，把f(x0)称为函数f(x)在D上的“下界”．

    (1)分别判断下列函数是否有“下界”？如果有，写出“下界”否则请说明理由；f1(x)＝1－2x(x＞0)，f2(x)＝x＋　x∈(0，5]

    (2)请你类比函数有“下界”的定义，写出函数f(x)在区间D上有“上界”的定义；并判断函数是否有“上界”？说明理由；

    (3)若函数f(x)在区间D上既有“上界”又有“下界”，则称函数f(x)是区间D上的“有界函数”，把“上界”减去“下界”的差称为函数f(x)在D上的“幅度M”．

    对于实数a，试探究函数F(x)＝x|x|－2x＋3是否是[a，a＋2]上的“有界函数”？如果是，求出“幅度M”的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    对于函数数学公式
    （1）探究函数f（x）的单调性，并给予证明；
    （2）是否存在实数a使函数f（x）为奇函数？
    （3）求函数f（x）的值域．

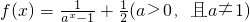
    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    对于函数数学公式
    （1）判断函数f（x）的奇偶性；
    （2）探究函数f（x）在（0，+∞）上的单调性，并用定义加以证明；
    （3）当2＜a＜4时，求函数f（x）在[-3，-1]上的最大值和最小值．

    查看答案和解析>>

    同步练习册答案