
如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1.
(1)设P为AC的中点.证明:在AB上存在一点Q,使PQ⊥OA,并计算 的值;
的值;
(2)求二面角O-AC-B的平面角的余弦值.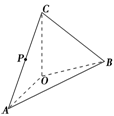
解:解法一:(1)在平面OAB内作ON⊥OA交AB于N,连结NC.
又OA⊥OC,∴OA⊥平面ONC.
∵NC?平面ONC,∴OA⊥NC.
取Q为AN的中点,则PQ∥NC,
∴PQ⊥OA.
在等腰△AOB中,∠AOB=120°,
∴∠OAB=∠OBA=30°.
在Rt△AON中,∠OAN=30°,
∴ON=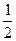 AN=AQ.
AN=AQ.
在△ONB中,∠NOB=120°-90°=30°=∠NBO,∴NB=ON=AQ,∴ =3.
=3.
(2)连结PN,PO.
由OC⊥OA,OC⊥OB知OC⊥平面OAB.
又ON?平面OAB,∴OC⊥ON.
又由ON⊥OA知ON⊥平面AOC.
∴OP是NP在平面AOC内的射影.
在等腰Rt△COA中,P为AC的中点,
∴AC⊥OP.
根据三垂线定理,知AC⊥NP.
∴∠OPN为二面角O-AC-B的平面角.在等腰Rt△COA中,OC=OA=1,
∴OP= .
.
在Rt△AON中,ON=OAtan 30°= ,
,
∴在Rt△PON中,PN= ,
,
∴cos ∠OPN= =
= .
.
解析


 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:
 如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1
如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1| AB | AQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
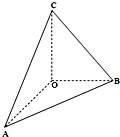 如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1
如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1.
如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1.| AB | AQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1.
如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1.| AB | AQ |
查看答案和解析>>
科目:高中数学 来源:2013届福建省上学期高二期中考试理科数学试卷 题型:解答题
如图,在四面体ABOC中,OC⊥OA,OC⊥OB,∠AOB=120°,且OA=OB=OC=1.
(1)设P为AC的中点.证明:在AB上存在一点Q,使PQ⊥OA,并计算 的值;
的值;
(2)求二面角O-AC-B的平面角的余弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com