
(本小题满分12分)设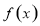 为定义在R上的偶函数,当
为定义在R上的偶函数,当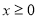 时,
时,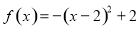 .
.
(1)求函数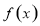 在R上的解析式;
在R上的解析式;
(2)在直角坐标系中画出函数 的图象;
的图象;
(3)若方程 -k=0有四个解,求实数k的取值范围.
-k=0有四个解,求实数k的取值范围.
(1)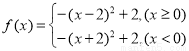 (2)见解析;(3)见解析
(2)见解析;(3)见解析
【解析】
试题分析:(1)第一步求函数解析式,由已知当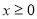 时,
时,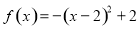 ,只需求出
,只需求出 时
时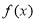 的解析式即可,可借助偶函数的定义联系
的解析式即可,可借助偶函数的定义联系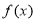 与
与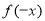 的关系得以解决;(2)在直角坐标系上,按着解析式的要求画出两抛物线相应的部分;(3)根据化归思想,把方程
的关系得以解决;(2)在直角坐标系上,按着解析式的要求画出两抛物线相应的部分;(3)根据化归思想,把方程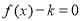 的实根个数问题转化为曲线
的实根个数问题转化为曲线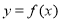 与直线
与直线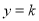 的交点个数问题,借助数形结合把问题解决.
的交点个数问题,借助数形结合把问题解决.
试题解析:(1)由已知当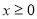 时,
时,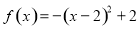 .只需求出
.只需求出 时
时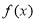 的解析式即可.
的解析式即可.
由于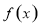 为定义在R上的偶函数,则
为定义在R上的偶函数,则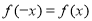 ,则
,则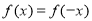 ;
;
若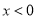 ,则
,则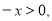
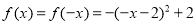
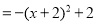 ,
,
则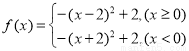 ;
;
图象如图所示
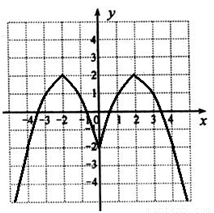
(3)由于方程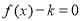 的解就是函数
的解就是函数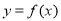 的图象与直线
的图象与直线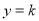 的交点的横坐标,观察函数
的交点的横坐标,观察函数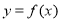 图象与直线
图象与直线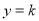 的交点情况可知,当
的交点情况可知,当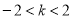 时,函数
时,函数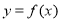 图象与直线
图象与直线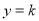 有四个交点,即方程
有四个交点,即方程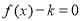 有四个解.
有四个解.
考点:1.函数的奇偶性;2.利用函数奇偶性求函数的解析式;3.数形结合研究函数图象的交点个数;


 科学实验活动册系列答案
科学实验活动册系列答案科目:高中数学 来源:2014-2015学年湖南省醴陵市、四中高一上学期期中考试数学试卷(解析版) 题型:选择题
.函数f (x)=-x2+4x+a,x∈[0,1],若f (x)有最小值-2,则f (x)的最大值为( )
A.-1 B.0 C.1 D.2
查看答案和解析>>
科目:高中数学 来源:2014-2015学年宁夏银川市高三上学期期中考试理科数学试卷(解析版) 题型:选择题
设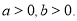 若
若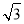 是
是 与
与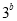 的等比中项,则
的等比中项,则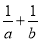 的最小值为 ( )
的最小值为 ( )
A. 8 B. 4 C. 1 D. 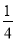
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com