
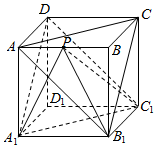
| A. | 平面ACB1∥平面A1C1D,且两平面的距离为$\frac{{\sqrt{3}}}{3}$ | |
| B. | 点P在线段AB上运动,则四面体PA1B1C1的体积不变 | |
| C. | 与所有12条棱都相切的球的体积为$\frac{{\sqrt{2}}}{3}$π | |
| D. | M是正方体的内切球的球面上任意一点,N是△AB1C外接圆的圆周上任意一点,则|MN|的最小值是$\frac{{\sqrt{3}-\sqrt{2}}}{2}$ |
分析 A.根据面面平行的判定定理以及平行平面的距离进行证明即可.
B.研究四面体的底面积和高的变化进行判断即可.
C.所有12条棱都相切的球的直径2R等于面的对角线B1C的长度,求出球半径进行计算即可.
D.根据正方体内切球和三角形外接圆的关系进行判断即可.
解答 解:A.∵AB1∥DC1,AC∥A1C1,且AC∩AB1=A,
∴平面ACB1∥平面A1C1D,
长方体的体对角线BD1=$\sqrt{3}$,
设B到平面ACB1的距离为h,
则${V}_{B-A{B}_{1}C}$=$\frac{1}{3}×\frac{1}{2}×1×1$×1=$\frac{1}{3}×\frac{1}{2}×$$\sqrt{2}×\sqrt{2}×\frac{\sqrt{3}}{2}$h,即h=$\frac{\sqrt{3}}{3}$,
则平面ACB1与平面A1C1D的距离d=$\sqrt{3}$-2h=$\sqrt{3}-2×\frac{\sqrt{3}}{3}$=$\frac{{\sqrt{3}}}{3}$,故A正确,
B.点P在线段AB上运动,则四面体PA1B1C1的高为1,底面积不变,则体积不变,故B正确,
C.与所有12条棱都相切的球的直径2R等于面的对角线B1C=$\sqrt{2}$,则2R=$\sqrt{2}$,R=$\frac{\sqrt{2}}{2}$,
则球的体积V=$\frac{4}{3}π{R}^{3}$=$\frac{4}{3}$×π×($\frac{\sqrt{2}}{2}$)3=$\frac{{\sqrt{2}}}{3}$π,故C正确,
D.设与正方体的内切球的球心为O,正方体的外接球为O′,
则三角形ACB1的外接圆是正方体的外接球为O′的一个小圆,
∵点M在与正方体的内切球的球面上运动,点N在三角形ACB1的外接圆上运动,
∴线段MN长度的最小值是正方体的外接球的半径减去正方体的内切球相切的球的半径,
∵正方体ABCD-A1B1C1D1的棱长为1,
∴线段MN长度的最小值是$\frac{\sqrt{3}}{2}$-$\frac{1}{2}$.故D错误,
故选:D.
点评 本题主要考查命题的真假判断,涉及空间几何体的结构,面面平行的判断,球的内切问题,涉及的知识点较多,综合性较强,难度较大.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -7 | B. | -6 | C. | -5 | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
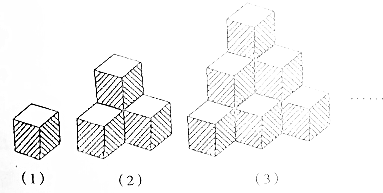 如图是由一些小正方体摞成的,第(1)堆有1个,第(2)堆有4个,第(3)堆有10个…,则第n堆有$\frac{n(n+1)(n+2)}{6}$小正方体.
如图是由一些小正方体摞成的,第(1)堆有1个,第(2)堆有4个,第(3)堆有10个…,则第n堆有$\frac{n(n+1)(n+2)}{6}$小正方体.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
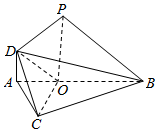 如图,∠ABC=$\frac{π}{4}$,O为AB上一点,3OB=3OC=2AB,PO⊥平面ABC,2DA=2AO=PO,OA=1,且DA∥PO.
如图,∠ABC=$\frac{π}{4}$,O为AB上一点,3OB=3OC=2AB,PO⊥平面ABC,2DA=2AO=PO,OA=1,且DA∥PO.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com