解:(I)解法一:a
2=2λ+λ
2+(2-λ)×2=λ
2+2
2,a
3=λ(λ
2+2
2)+λ
3+(2-λ)×2
2=2λ
3+2
3,
a
4=λ(2λ
3+2
3)+λ
4+(2-λ)×2
3=3λ
4+2
4.
由此可猜想出数列{a
n}的通项公式为a
n=(n-1)λ
n+2
n.
以下用数学归纳法证明.
(1)当n=1时,a
1=2,等式成立.
(2)假设当n=k时等式成立,即a
k=(k-1)λ
k+2
k,
那么,a
k+1=λa
k+λ
k+1+(2-λ)2
k=λ(k-1)λ
k+λ2
k+λ
k+1+2
k+1-λ2
k=[(k+1)-1]λ
k+1+2
k+1.
这就是说,当n=k+1时等式也成立.根据(1)和(2)可知,等式a
n=(n-1)λ
n+2
n对任何n∈N
*都成立.
解法二:由a
n+1=λa
n+λ
n+1+(2-λ)2
n(n∈N*),λ>0,可得
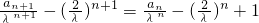
,
所以

为等数列,其公差为1,首项为0.故
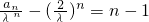
,
所以数列{a
n}的通项公式为a
n=(n-1)λ
n+2
n.
(II)解:设T
n=λ
2+2λ
3+3λ
4++(n-2)λ
n-1+(n-1)λ
n①
λT
n=λ
3+2λ
4+3λ
5++(n-2)λ
n+(n-1)λ
n+1.②
当λ≠1时,①式减去②式,得(1-λ)T
n=λ
2+λ
3++λ
n-(n-1)λ
n+1=
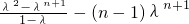
,

这时数列{a
n}的前n项和

当λ=1时,
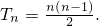
这时数列{a
n}的前n项和
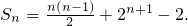
(III)证明:通过分析,推测数列
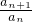
的第一项

最大.下面证明:

③
由λ>0知a
n>0.要使③式成立,只要2a
n+1<(λ
2+4)a
n(n≥2).因为(λ
2+4)a
n=(λ
2+4)(n-1)λ
n+(λ
2+4)2
n>4λ.(n-1)λ
n+4×2
n=4(n-1)λ
n+1+2
n+2≥2nλ
n+1+2
n+2=2a
n+1,n>2.
所以③式成立.因此,存在k=1,使得
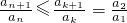
对任意n∈N
*均成立.
分析:(I)解法一:由题设条件可猜想出数列{a
n}的通项公式为a
n=(n-1)λ
n+2
n.然后用数学归纳法证明.
解法二:由a
n+1=λa
n+λ
n+1+(2-λ)2
n(n∈N*),λ>0,可知

为等数列,其公差为1,首项为0.由此可求出数列{a
n}的通项公式.
(II)设T
n=λ
2+2λ
3+3λ
4++(n-2)λ
n-1+(n-1)λ
n,λT
n=λ
3+2λ
4+3λ
5++(n-2)λ
n+(n-1)λ
n+1.然后用错位相减法进行求解.(III)证明:通过分析,推测数列
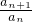
的第一项

最大.然后用分析法进行证明.
点评:本题以数列的递推关系式为载体,主要考查等比数列的前n项和公式、数列求和、不等式的证明等基础知识与基本方法,考查归纳、推理、运算及灵活运用数学知识分析问题和解决问题的能力.

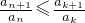 对任意n∈N*均成立.
对任意n∈N*均成立.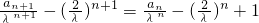 ,
, 为等数列,其公差为1,首项为0.故
为等数列,其公差为1,首项为0.故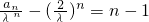 ,
,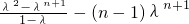 ,
,

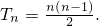 这时数列{an}的前n项和
这时数列{an}的前n项和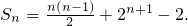
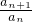 的第一项
的第一项 最大.下面证明:
最大.下面证明: ③
③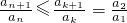 对任意n∈N*均成立.
对任意n∈N*均成立. 为等数列,其公差为1,首项为0.由此可求出数列{an}的通项公式.
为等数列,其公差为1,首项为0.由此可求出数列{an}的通项公式.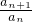 的第一项
的第一项 最大.然后用分析法进行证明.
最大.然后用分析法进行证明.

 中考解读考点精练系列答案
中考解读考点精练系列答案 ,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn=
,并且对任意n∈N*,n≥2都有an•an-1=an-1-an成立,令bn= (n∈N*).
(n∈N*). }的前n项和为Tn,证明:
}的前n项和为Tn,证明: .
.