
解法一:设抛物线y=ax2-1上关于x+y=0对称的相异两点坐标为A(x0,y0)、B(-y0,-x0).
∵两点都在抛物线上,
∴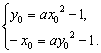
![]()
①-②,得y0+x0=a(x02-y02).
∵x0+y0≠0,∴x0=![]() . ③
. ③
③代入②,得a2y02+ay0+1-a=0.
∵y0∈R,且(x0,y0),(-y0,-x0)相异,
∴Δ=a2-4a2(1-a)>0.
∴a>![]() .∴a的取值范围是(
.∴a的取值范围是(![]() ,+∞).
,+∞).
解法二:设抛物线上关于直线x+y=0对称的两点所在直线方程为y=x+b,代入y=ax2-1,得ax2-x-b-1=0.
∵x∈R,且两点为相异两点,
∴Δ=1+4a(b+1)>0,
即4ab+4a+1>0. ①
设两对称点为A(x1,y1)、B(x2,y2),则
x1+x2=![]() ,y1+y2=
,y1+y2=![]() +2b.
+2b.
又∵![]() +
+![]() =0,
=0,
∴![]() +
+![]() +b=0,即b=-
+b=0,即b=-![]() . ②
. ②
②代入①,得a>![]() .
.
∴a的取值范围是(![]() ,+∞).
,+∞).


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com