
设函数f(x)=asin(kx+![]() ),g(x)=btan(kx-
),g(x)=btan(kx-![]() )(k>0),它们的最小正周期分别为T1、T2,且T1+T2=
)(k>0),它们的最小正周期分别为T1、T2,且T1+T2=![]() ,已知f(
,已知f(![]() )=g(
)=g(![]() ),f(
),f(![]() )=-3g(
)=-3g(![]() )+1.
)+1.
(1)求f(x),g(x)的解析式;
(2)f(x)的图象可由函数y=sinx(x∈R)的图象经过怎样的平移伸缩变换得到?
|
思路分析:考查三角函数的性质及三角函数图象的变换,可根据题目的条件确定a、b、k的值. 解:(1)由已知可得 整理得 解得 所以f(x)=sin(2x+ (2)方法一:将函数y=sinx(x∈R)的图象向左平移 方法二:将函数y=sinx(x∈R)图象上所有点的横坐标变为原来的 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:黄冈重点作业·高三数学(下) 题型:044
设函数f(x)=asin(kx+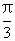 )和g(x)=btan(kx-
)和g(x)=btan(kx-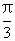 )(a>0,b>0,k>0),若它们的最小正周期之和为
)(a>0,b>0,k>0),若它们的最小正周期之和为 ,且f(
,且f( )=g(
)=g( ),f(
),f( )=-
)=- g(
g( )+1,求f(x)、g(x)的解析式.
)+1,求f(x)、g(x)的解析式.
查看答案和解析>>
科目:高中数学 来源:江苏金练·高中数学、全解全练、数学必修4 题型:044
设函数f(x)=asin(πx+α)+bcos(πx+β),其中a、b、α、β均为非零实数,且满足f(2002)=1.求f(2003)的值.
查看答案和解析>>
科目:高中数学 来源:山东省郓城一中2012届高三上学期寒假作业数学试卷(9) 题型:044
设函数f(x)=Asin(ωx+φ)(A>0,ω>0,|ω|≤π)的图象的最高点D的坐标为(2,![]() ),由最高点运动到最低相邻最低点F时,曲线与x轴相交于点E(6,0),
),由最高点运动到最低相邻最低点F时,曲线与x轴相交于点E(6,0),
(1)求A、ω、![]() 的值,
的值,
(2)求函数y=g(x),使其图象与y=f(x)图象关于直线x=8对称.
查看答案和解析>>
科目:高中数学 来源:2012年普通高等学校招生全国统一考试重庆卷数学文科 题型:044
设函数f(x)=Asin(ωx+![]() )(其中A>0,ω>0,-π<
)(其中A>0,ω>0,-π<![]() <π)在x=
<π)在x=![]() 处取得最大值2,其图象与轴的相邻两个交点的距离为
处取得最大值2,其图象与轴的相邻两个交点的距离为![]()
(Ⅰ)求f(x)的解析式;
(Ⅱ)求函数g(x)=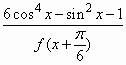 的值域.
的值域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com