设{an}是公比q>1的等比数列,Sn为其前n项和,s3=7,a1+3,3a2,a3+4构成等差数列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足bn=n+lna3n+1(n∈N*),求数列{bn}的前n项和Tn.
解:(1)由题意s
3=7,且a
1+3,3a
2,a
3+4构成等差数列,可得
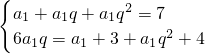
,解得
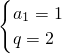
,或
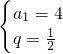
.
再由公比q>1可得
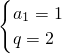
,∴a
n=2
n-1 (n∈N
*).
(2)由于数列{b
n}满足b
n=n+lna
3n+1(n∈N
*),即b
n=n+ln2
3n=n(3ln2+1),∴b
n+1 =(n+1)(3ln2+1),
∴b
n+1-b
n=3ln2+1 为常数,故数列{b
n}是以 3ln2+1为首项,以 3ln2+1为公差的等差数列.
∴数列{b
n}的前n项和Tn=
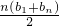
=
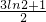
(n
2+n).
分析:(1)由题意s
3=7,且a
1+3,3a
2,a
3+4构成等差数列,求出首项和公比,从而求得数列{a
n}的通项公式.
(2)化简b
n为 n(3ln2+1),可得数列{b
n}是以 3ln2+1为首项,以 3ln2+1为公差的等差数列,根据等差数列的前n项和公式求出数列{b
n}的前n项和Tn 的值.
点评:本题主要考查等差数列的定义和性质,等差数列的前n项和公式,等差关系的确定,等比数列的通项公式,属于中档题.

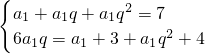 ,解得
,解得 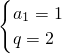 ,或
,或 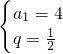 .
.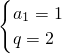 ,∴an=2n-1 (n∈N*).
,∴an=2n-1 (n∈N*).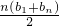 =
=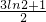 (n2+n).
(n2+n).

 发散思维新课堂系列答案
发散思维新课堂系列答案 N*),求数列{bn}的前n项和Tn.
N*),求数列{bn}的前n项和Tn.