
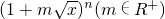 展开式的二项式系数之和为256,展开式中含x项的系数为112.
展开式的二项式系数之和为256,展开式中含x项的系数为112.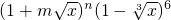 展开式中含x2项的系数.
展开式中含x2项的系数.
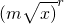 =
= mr
mr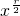 …3分
…3分 =1,即r=2,…4分
=1,即r=2,…4分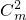 m2=112,解得m=±2…6分
m2=112,解得m=±2…6分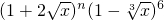 展开式的通项为
展开式的通项为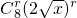 •
•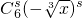 ,即
,即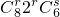
 (其中r=0,1,2,…8;s=0,2,…6),…9分
(其中r=0,1,2,…8;s=0,2,…6),…9分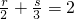 ,则3r+2s=12…10分
,则3r+2s=12…10分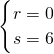 或
或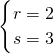 或
或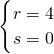 …12分
…12分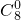 (-1)6+
(-1)6+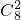 22
22 (-1)3+
(-1)3+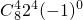 =-1119…14分
=-1119…14分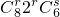
 可含求得x2项的系数.
可含求得x2项的系数.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com