
 时,设函数f(x)表示实数x与x的相应给定区间内整数之差的绝对值.现给出下列关于函数f(x)的四个命题:
时,设函数f(x)表示实数x与x的相应给定区间内整数之差的绝对值.现给出下列关于函数f(x)的四个命题: ];
]; (k∈Z)对称;
(k∈Z)对称; ,
, ]上是增函数.
]上是增函数.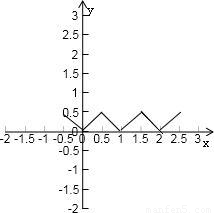 解:由题意函数f(x)表示实数x与x的相应给定区间内整数之差的绝对值,
解:由题意函数f(x)表示实数x与x的相应给定区间内整数之差的绝对值, <x≤
<x≤ ,f(x)=|x|,
,f(x)=|x|, <x≤1+
<x≤1+ ,f(x)=|x-1|,
,f(x)=|x-1|, <x≤2+
<x≤2+ ,f(x)=|x-2|,分别作出它们的图象,如图所示.
,f(x)=|x-2|,分别作出它们的图象,如图所示.

科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省揭阳三中高一(下)第三次段考数学试卷(解析版) 题型:解答题
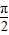 )的最高点D的坐标为(
)的最高点D的坐标为(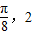 ),由最高点D运动到相邻最低点时,函数图形与x的交点的坐标为(
),由最高点D运动到相邻最低点时,函数图形与x的交点的坐标为(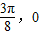 );
);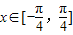 时,求函数f(x)的最大值和最小值以及分别取得最大值和最小值时相应的自变量x的值.
时,求函数f(x)的最大值和最小值以及分别取得最大值和最小值时相应的自变量x的值.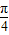 个单位,得到函数y=g(x)的图象,求函数y=g(x)的单调减区间.
个单位,得到函数y=g(x)的图象,求函数y=g(x)的单调减区间.查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市昌平区高三(上)期末数学试卷(文科)(解析版) 题型:解答题
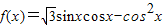 .
.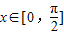 时,求函数f(x)的最大值和最小值.
时,求函数f(x)的最大值和最小值.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 时,设函数f(x)表示实数x与x的相应给定区间内整数之差的绝对值.现给出下列关于函数f(x)的四个命题:
时,设函数f(x)表示实数x与x的相应给定区间内整数之差的绝对值.现给出下列关于函数f(x)的四个命题: ];
]; (k∈Z)对称;
(k∈Z)对称; ,
, ]上是增函数.
]上是增函数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com