
已知函数f(x)=sin(ωx+φ)(ω>0,0<φ<π)的周期为π,图像的一个对称中心为![]() ,将函数f(x)图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移
,将函数f(x)图像上的所有点的横坐标伸长为原来的2倍(纵坐标不变),在将所得图像向右平移![]() 个单位长度后得到函数g(x)的图像.
个单位长度后得到函数g(x)的图像.
(1)求函数f(x)与g(x)的解析式;
(2)是否存在![]() ,使得f(x0),g(x0),f(x0)g(x0)按照某种顺序成等差数列?若存在,请确定x0的个数;
,使得f(x0),g(x0),f(x0)g(x0)按照某种顺序成等差数列?若存在,请确定x0的个数;
若不存在,说明理由.
(3)求实数a与正整数n,使得F(x)=f(x)+ag(x)在(0,nπ)内恰有2013个零点.
本小题主要考查同角三角函数的基本关系.三角恒等变换.三角函数的图像与性质.函数.函数的导数.函数的零点.不等式等基础知识,考查运算求解能力.抽象概括能力,考查函数与方程思想,数形结合思想,分类与整合思想.化归与转化思想,满分14分.
解:(Ⅰ)由函数f(x)=sin(ωx+Φ)的周期为π,ω>0,得ω=2
又曲线y=f(x)的一个对称中心为![]() ,
,![]()
故![]() ,得
,得![]() ,所以f(x)=cos2x
,所以f(x)=cos2x
将函数f(x)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变)后可得y=cosx的图象,再将y=cosx的图象向右平移![]() 个单位长度后得到函数g(x)=sinx
个单位长度后得到函数g(x)=sinx
(Ⅱ)当![]() 时,
时,![]() ,
,![]()
所以sinx>cos2x>sinxcos2x
问题转化为方程2cos2x=sinx+sinxcos2x在![]() 内是否有解
内是否有解
设G(x)=sinx+sinxcos2x-2cos2x,![]()
则![]()
因为![]() ,所以
,所以![]() ,G(x)在
,G(x)在![]() 内单调递增
内单调递增
又![]() ,
,![]()
且函数G(x)的图象连续不断,故可知函数G(x)在![]() 内存在唯一零点x0,
内存在唯一零点x0,
即存在唯一的![]() 满足题意
满足题意
(Ⅲ)依题意,F(x)=asinx+cos2x,令F(x)=asinx+cos2x=0
当sinx=0,即x=kπ(k∈Z)时,cos2x=1,从而x=kπ(k∈Z)不是方程F(x)=0的解,所以方程F(x)=0等价于关于x的方程![]() ,
,![]()
现研究![]() 时方程解的情况
时方程解的情况
令![]() ,
,![]()
则问题转化为研究直线y=a与曲线y=h(x)在![]() 的交点情况
的交点情况
![]() ,令
,令![]() ,得
,得![]() 或
或![]()
当x变化时,h(x)和![]() 变化情况如下表
变化情况如下表
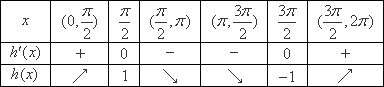
当x>0且x趋近于0时,h(x)趋向于-∞
当x<π且x趋近于π时,h(x)趋向于-∞
当x>π且x趋近于π时,h(x)趋向于+∞
当x<2π且x趋近于2π时,h(x)趋向于+∞
故当a>1时,直线y=a与曲线y=h(x)在(0,π)内有无交点,在(π,2π)内有2个交点;
当a<-1时,直线y=a与曲线y=h(x)在(0,π)内有2个交点,在(π,2π)内无交点;
当-1<a<1时,直线y=a与曲线y=h(x)在(0,π)内有2个交点,在(π,2π)内有2个交点
由函数h(x)的周期性,可知当a≠±1时,直线y=a与曲线y=h(x)在(0,nπ)内总有偶数个交点,从而不存在正整数n,使得直线y=a与曲线y=h(x)在(0,nπ)内恰有2013个交点;当a=±1时,直线y=a与曲线y=h(x)在![]() 内有3个交点,由周期性,2013=3×671,所以n=671×2=1342
内有3个交点,由周期性,2013=3×671,所以n=671×2=1342
综上,当a=±1,n=1342时,函数F(x)=f(x)+ag(x)在(0,nπ)内恰有2013个零点


科目:高中数学 来源:云南省昆明一中2010届高三上学期期中考试数学文科试题 题型:044
已知函数f(x)=![]() x3+ax2+bx+c
x3+ax2+bx+c
(Ⅰ)若函数f(x)在x=1时有极值且在函数图象上的点(0,1)处的切线与直线3x+y=0平行,求f(x)的解析式;
(Ⅱ)当f(x)在x∈(0,1)取得极大值且在x∈(1,2)取得极小值时,设点M(b-2,a+1)所在平面区域为S,经过原点的直线L将S分为面积比为1∶3的两部分,求直线L的方程.
查看答案和解析>>
科目:高中数学 来源:广东省广州市2012届高三第一次模拟考试数学文科试题 题型:044
已知函数f(x)=-x3+ax2+b(a,b∈R).
(1)求函数f(x)的单调递增区间;
(2)若对任意a∈[3,4],函数f(x)在R上都有三个零点,求实数b的取值范围.
已知椭圆x2+![]() =1的左、右两个顶点分别为A、B.曲线C是以A、B两点为顶点,离心率为
=1的左、右两个顶点分别为A、B.曲线C是以A、B两点为顶点,离心率为![]() 的双曲线,设点P在第一象限且在曲线C上,直线AP与椭圆相交于另一点T.
的双曲线,设点P在第一象限且在曲线C上,直线AP与椭圆相交于另一点T.
(1)求曲线C的方程;
(2)设点P、T的横坐标分别为x1,x2,证明:x1·x2=1;
(3)设△TAB与△POB(其中O为坐标原点)的面积分别为S1与S2,且![]() ,求S
,求S![]() -S
-S![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:福建省师大附中2012届高三高考模拟数学文科试题 题型:044
已知函数f(x)=x3+ax2+bx(x≠0)只有一个零点x=3.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若函数![]() 在区间(0,2)上有极值点,求m取值范围;
在区间(0,2)上有极值点,求m取值范围;
(Ⅲ)是否存在两个不等正数s,t(s<t),当x∈[s,t]时,函数f(x)=x3+ax2+bx的值域也是[s,t],若存在,求出所有这样的正数s,t;若不存在,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=ax3+![]() x2在x=-1处取得极值,记g(x)=
x2在x=-1处取得极值,记g(x)=![]() ,程序框图如图所示,若输出的结果S>
,程序框图如图所示,若输出的结果S>![]() ,则判断框中可以填入的关于n的判断条件是 ( )
,则判断框中可以填入的关于n的判断条件是 ( )

A.n≤2 011? B.n≤2 012?
C.n>2 011? D.n>2 012?
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西赣州四所重点中学高三上学期期末联考理数学试卷(解析版) 题型:选择题
已知函数f(x)=ax3+ x2在x=-1处取得极大值,记g(x)=
x2在x=-1处取得极大值,记g(x)= 。程序框图如图所示,若输出的结果S=
。程序框图如图所示,若输出的结果S= ,则判断框中可以填入的关于n的判断条件是( )
,则判断框中可以填入的关于n的判断条件是( )

A.n≤2013 B.n≤2014 C.n>2013 D.n>2014
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com