
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 |  | 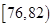 |  |  | 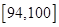 |
| 元件A | 8 | 12 | 40 | 32] | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
(1) ;(2)
;(2) 详见解析.
详见解析.
解析试题分析:(1)由题设条件能求出元件 为正品的概率和元件
为正品的概率和元件 为正品的概率.
为正品的概率.
(2)(i)设生产的5件元件中正品件数为 ,则有次品
,则有次品 件,由题意知
件,由题意知 ,由此能求出生产5件元件B所获得的利润不少于300元的概率.
,由此能求出生产5件元件B所获得的利润不少于300元的概率.
(ii)随机变量 的所有取值为
的所有取值为 ,分别求出
,分别求出 ,
, ,
, ,
,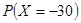 ,由此能求出
,由此能求出 的分布列和
的分布列和 .
.
试题解析:(1)由题可知元件A为正品的概率为 ,元件B为正品的概率为
,元件B为正品的概率为 。 2分
。 2分
(2)(i)设生产的5件元件中正品件数为 ,则有次品5
,则有次品5 件,由题意知
件,由题意知 得到
得到 ,设“生产5件元件B所获得的利润不少于300元”为事件
,设“生产5件元件B所获得的利润不少于300元”为事件 ,则
,则 。 6分
。 6分
(ii)随机变量 的所有取值为150,90,30,-30,
的所有取值为150,90,30,-30,
则 ,
, ,
, ,
, ,所以
,所以 的分布列为:
的分布列为:
10分
150 90 30 -30 





 12分
12分
考点:1.古典概型的概率问题;2.离散型随机变量的分布列与期望.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:高中数学 来源: 题型:解答题
已知函数 .
.
(1)从区间 内任取一个实数
内任取一个实数 ,设事件
,设事件 ={函数
={函数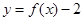 在区间
在区间 上有两个不同的零点},求事件
上有两个不同的零点},求事件 发生的概率;
发生的概率;
(2)若连续掷两次骰子(骰子六个面上标注的点数分别为 )得到的点数分别为
)得到的点数分别为 和
和 ,记事件
,记事件 {
{ 在
在 恒成立},求事件
恒成立},求事件 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某篮球队与其他6支篮球队依次进行6场比赛,每场均决出胜负,设这支篮球队与其他篮球队比赛胜场的事件是独立的,并且胜场的概率是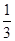 .
.
(1)求这支篮球队首次胜场前已经负了两场的概率;
(2)求这支篮球队在6场比赛中恰好胜了3场的概率;
(3)求这支篮球队在6场比赛中胜场数的期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
A高校自主招生设置了先后三道程序:部分高校联合考试、本校专业考试、本校面试.在每道程序中,设置三个成绩等级:优、良、中.若考生在某道程序中获得“中”,则该考生在本道程序中不通过,且不能进入下面的程序.考生只有全部通过三道程序,自主招生考试才算通过.某中学学生甲参加A高校自主招生考试,已知该生在每道程序中通过的概率均为 ,每道程序中得优、良、中的概率分别为p1、
,每道程序中得优、良、中的概率分别为p1、 、p2.
、p2.
(1)求学生甲不能通过A高校自主招生考试的概率;
(2)设X为学生甲在三道程序中获优的次数,求X的概率分布及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲、乙、丙、丁4名同学被随机地分到 三个社区参加社会实践,要求每个社区至少有一名同学.
三个社区参加社会实践,要求每个社区至少有一名同学.
(1)求甲、乙两人都被分到 社区的概率;
社区的概率;
(2)求甲、乙两人不在同一个社区的概率;
(3)设随机变量 为四名同学中到
为四名同学中到 社区的人数,求
社区的人数,求 的分布列和
的分布列和 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学为丰富教工生活,国庆节举办教工趣味投篮比赛,有 、
、 两个定点投篮位置,在
两个定点投篮位置,在 点投中一球得2分,在
点投中一球得2分,在 点投中一球得3分.其规则是:按先
点投中一球得3分.其规则是:按先 后
后 再
再 的顺序投
的顺序投
篮.教师甲在 和
和 点投中的概率分别是
点投中的概率分别是 ,且在
,且在 、
、 两点投中与否相互独立.
两点投中与否相互独立.
(1)若教师甲投篮三次,试求他投篮得分X的分布列和数学期望;
(2)若教师乙与甲在A、B点投中的概率相同,两人按规则各投三次,求甲胜乙的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某篮球队与其他6支篮球队依次进行6场比赛,每场均决出胜负,设这支篮球队与其他篮球队比赛胜场的事件是独立的,并且胜场的概率是 .
.
(1)求这支篮球队首次胜场前已经负了两场的概率;
(2)求这支篮球队在6场比赛中恰好胜了3场的概率;
(3)求这支篮球队在6场比赛中胜场数的期望和方差.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,∠AOB=60°,OA=2,OB=5,在线段OB上任取一点C,试求: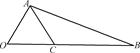
(1)△AOC为钝角三角形的概率;
(2)△AOC为锐角三角形的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com