
����Ŀ����֪����![]() ��
�� ![]() .
.
��1������![]() ����С�����ڣ�
����С�����ڣ�
��2����![]() ����
����![]() ����
����![]() ��ֵ.
��ֵ.
���𰸡�(1) ![]() (2)
(2) ![]()
���������������:(1)���ݶ����ǹ�ʽ�����ǺͲʽ�õ�![]() �������õ����ڣ���2����
�������õ����ڣ���2����![]() ���õ�
���õ�![]() ��
�� ![]() ������սǹ�ʽ�õ�
������սǹ�ʽ�õ�![]() ������ֵ�õ�����ֵ.
������ֵ�õ�����ֵ.
������
��1��������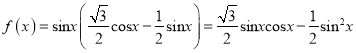
![]() =
=![]()
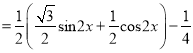
![]()
����![]() ����С������Ϊ
����С������Ϊ![]() ��
��
��2����![]()
![]()
����![]() ��
��![]() ������
������![]()
��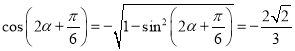 ��
��
��![]()
![]()
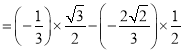
![]()
�����͡������
��������
20
����Ŀ��Ϊ��Ӧʮ�Ŵ������ʵʩ�������ս�ԣ�ij��ׯͶ��![]() ��Ԫ������һ����ɫũ��Ʒ�ӹ���.��Ӫ�У���һ��֧��
��Ԫ������һ����ɫũ��Ʒ�ӹ���.��Ӫ�У���һ��֧��![]() ��Ԫ���Ժ�ÿ���֧������һ��������
��Ԫ���Ժ�ÿ���֧������һ��������![]() ��Ԫ���ӵ�һ����ÿ��ũ��Ʒ��������Ϊ
��Ԫ���ӵ�һ����ÿ��ũ��Ʒ��������Ϊ![]() ��Ԫ��ǰ
��Ԫ��ǰ![]() ��Ĵ������ۺ�=ǰ
��Ĵ������ۺ�=ǰ![]() ��� ������-ǰ
��� ������-ǰ![]() �����֧��-Ͷ�ʶ�
�����֧��-Ͷ�ʶ�![]() ��Ԫ��.
��Ԫ��.
��1���ó��ӵڼ��꿪ʼӯ����
��2���ó��ڼ�����ƽ��������ﵽ��������ƽ������������ֵ.
���𰸡�(1) �ӵ�![]() ��ʼӯ��(2) �ó���
��ʼӯ��(2) �ó���![]() ����ƽ��������ﵽ�����ƽ�����������ֵΪ
����ƽ��������ﵽ�����ƽ�����������ֵΪ![]() ��Ԫ
��Ԫ
�����������������(1)���ݹ�ʽ�õ�![]() �����ֵ����0��ò�����Χ����2�����ݹ�ʽ�õ�
�����ֵ����0��ò�����Χ����2�����ݹ�ʽ�õ�![]() ���ɾ�ֵ����ʽ�õ�������ֵ.
���ɾ�ֵ����ʽ�õ�������ֵ.
������
�������֪ǰ![]() ��Ĵ������ܺ�
��Ĵ������ܺ�
![]()
��1����![]() ����
����![]() �����
�����![]()
��![]() ֪���ӵ�
֪���ӵ�![]() ��ʼӯ��.
��ʼӯ��.
��2����ƽ��������![]()
��Ϊ![]() ����
����![]()
����![]()
���ҽ���![]() ����
����![]() ʱ�Ⱥų���.
ʱ�Ⱥų���.
��ƽ�����������ֵΪ![]() ��Ԫ��
��Ԫ��
�ʸó���![]() ����ƽ��������ﵽ�����ƽ�����������ֵΪ
����ƽ��������ﵽ�����ƽ�����������ֵΪ![]() ��Ԫ.
��Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����A-BCDE��,����BCDEΪֱ������,CD��ƽ��ABC,����ABCD�ǵ���ֱ��������,��EBC=��ABC=90��,BC=CD=2BE,��M����AD���е�
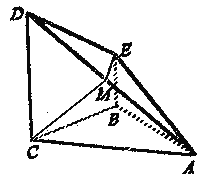
(1)������ֱ��ME��AB���ɽǵĴ�С;
(��)֤��:ƽ��AED��ƽ��ACD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������ϵ�ļ�����ֱ������ϵ��ԭ���غϣ�������x��ķǸ������غϣ�������C�ļ����귽��Ϊ��=6cos��+2sin�ȣ�ֱ��l�IJ�������Ϊ ![]() ��tΪ��������
��t��������
��1��������C��ֱ�����귽����ֱ��l����ͨ���̣�
��2�����Q��1��2����ֱ��l������C����A��B���㣬��|QA||QB|��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x�IJ���ʽa��ax��ex��2x��1����a����1�����ҽ������������⣬��ʵ��a��ȡֵ��ΧΪ�� ��
A.���� ![]() ��
�� ![]() ]
]
B.����1�� ![]() ]
]
C.���� ![]() ����
���� ![]() ]
]
D.���� ![]() ����
���� ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ҵ�������˶�Ա����15000�ˣ��������˶�Ա9000�ˣ�Ů�˶�Ա6000�ˣ�Ϊ����õ���ҵ�������˶�Աÿ��ƽ��������ռ��ʱ�����������÷ֲ�����ķ������ռ�300λҵ�������˶�Աÿ��ƽ��������ռ��ʱ����������ݣ���λ��Сʱ��
�õ�ҵ�������˶�Աÿ��ƽ����������ռ��ʱ���Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ���������������ݷ�������Ϊ����0��2]����2��4]����4��6]����6��8]����8��10]����10��12]��
����ҵ���˶�Ա��ÿ��ƽ��������ʱ����ռ��ʱ�䳬��4Сʱ��
����Ϊ���Ȱ�����
����K2= ![]()
P��K2��k0�� | 0.10 | 0.05 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 6.635 | 7.879 |
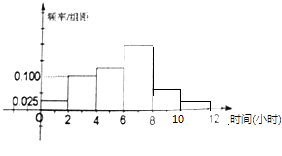
��1��Ӧ�ռ�����λŮ�˶�Ա�������ݣ�
��2�����Ƹõ���ÿ��ƽ����������ռ��ʱ�䳬��4��Сʱ�ĸ��ʣ�
��3�������������У���80λŮ�˶�Ա���Ȱ������뻭�����Ȱ��������Ա������������ж��Ƿ���99%�İ�����Ϊ���Ȱ��������Ա��йء���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() �Ƕ�����
�Ƕ�����![]() �ϵ��溯������
�ϵ��溯������![]() .
.
��1��ȷ��![]() �Ľ���ʽ��
�Ľ���ʽ��
��2���жϲ�֤��![]() ��
��![]() �ϵĵ����ԣ�
�ϵĵ����ԣ�
��3���ⲻ��ʽ![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��ʾ������ͬ��ƽ����
��ʾ������ͬ��ƽ���� ![]() ��ʾ������ֱͬ����������������������
��ʾ������ֱͬ����������������������
����![]() ������
������![]() ���ǡ�
���ǡ�![]() ���ij�ֲ���Ҫ������
���ij�ֲ���Ҫ������
����![]() ������
������![]() ���ǡ�
���ǡ�![]() ��
��![]() ���ij�Ҫ����.�ж���ȷ���ǣ� ��
���ij�Ҫ����.�ж���ȷ���ǣ� ��
A. �٢ڶ��������� B. ���������⣬���Ǽ�����
C. ���Ǽ����⣬���������� D. �٢ڶ��Ǽ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �Ƕ�����
�Ƕ�����![]() �ϵ�ż�������ҵ�
�ϵ�ż�������ҵ�![]() ʱ��
ʱ�� ![]() �����ѻ�������
�����ѻ�������![]() ��
��![]() ������ͼ����ͼ��ʾ��������ͼ��
������ͼ����ͼ��ʾ��������ͼ��

��1��ֱ��д������![]() ��
�� ![]() �������䣻
�������䣻
��2�������![]() ��
�� ![]() �Ľ���ʽ��
�Ľ���ʽ��
��3��������![]() ��
�� ![]() ������
������![]() ����Сֵ.
����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() Ϊż�������Һ���
Ϊż�������Һ���![]() ͼ��������ڶԳ����ľ���Ϊ
ͼ��������ڶԳ����ľ���Ϊ![]() .
.
��1����![]() ��ֵ��
��ֵ��
��2������![]() �ĶԳ��᷽�̣�
�ĶԳ��᷽�̣�
��3����![]() ʱ������
ʱ������![]() ��������ͬ��ʵ������m��ȡֵ��Χ��
��������ͬ��ʵ������m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com