
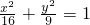 有一个交点?有两个交点?没有交点?当它们有一个交点时,画出它的图象.
有一个交点?有两个交点?没有交点?当它们有一个交点时,画出它的图象.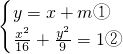
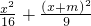 =1,
=1,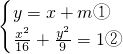 ,①代入②得
,①代入②得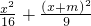 =1,其判别式为△=576(25-m2).由此可知直线与椭圆有一个交点的充要条件是m=±5,这时直线与椭圆相切.直线与椭圆有两个交点的充要条件是:-m2+25>0即|m|<5,这时直线与椭圆相割.直线与椭圆没有交点的充要条件是:-m2+25<0,即|m|>5.
=1,其判别式为△=576(25-m2).由此可知直线与椭圆有一个交点的充要条件是m=±5,这时直线与椭圆相切.直线与椭圆有两个交点的充要条件是:-m2+25>0即|m|<5,这时直线与椭圆相割.直线与椭圆没有交点的充要条件是:-m2+25<0,即|m|>5.

科目:高中数学 来源:1977年北京市高考数学试卷(理科)(解析版) 题型:解答题
 有一个交点?有两个交点?没有交点?当它们有一个交点时,画出它的图象.
有一个交点?有两个交点?没有交点?当它们有一个交点时,画出它的图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com