
 元,并且每件产品需向总公司交
元,并且每件产品需向总公司交 元(
元( )的管理费,预计当每件产品的售价为
)的管理费,预计当每件产品的售价为 元(
元( )时,一年的销售量为
)时,一年的销售量为 万件.
万件. (万元)与每件产品的售价
(万元)与每件产品的售价 的函数关系式;
的函数关系式; 最大,并求出
最大,并求出 的最大值
的最大值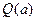 .
.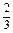 a或x=12(不合题意,舍去).
a或x=12(不合题意,舍去).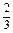 a≤
a≤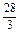 .
.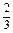 a两侧L′的值由正变负.
a两侧L′的值由正变负.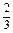 a<9即3≤a<
a<9即3≤a<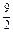 时,
时,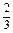 a≤
a≤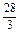 即
即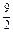 ≤a≤5时,
≤a≤5时,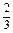 a)=(6+
a)=(6+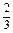 a-3-a)[12-(6+
a-3-a)[12-(6+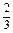 a)]2
a)]2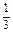 a)3.
a)3.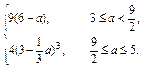
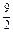 ,则当每件售价为9元时,分公司一年的利润L最大,最大值Q(a)=9(6-a)(万元);若
,则当每件售价为9元时,分公司一年的利润L最大,最大值Q(a)=9(6-a)(万元);若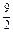 ≤a≤5,则当每件售价为(6+
≤a≤5,则当每件售价为(6+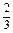 a)元时,分公司一年的利润L最大,最大值Q(a)=4(3-
a)元时,分公司一年的利润L最大,最大值Q(a)=4(3-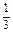 a)3(万元).
a)3(万元).

科目:高中数学 来源:不详 题型:填空题
 在
在 上是减函数,在
上是减函数,在 上是增函数;函数
上是增函数;函数 在
在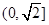 上是减函数,在
上是减函数,在 上是增函数;函数
上是增函数;函数 在
在 上是减函数,在
上是减函数,在 上是增函数;……利用上述所提供的信息解决问题:若函数
上是增函数;……利用上述所提供的信息解决问题:若函数 的值域是
的值域是 ,则实数
,则实数 的值是 .
的值是 .查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
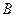 与
与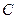 的距离,由于地形的限制,需要在岸上选取
的距离,由于地形的限制,需要在岸上选取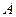 和
和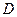 两点,现测得
两点,现测得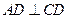 ,
,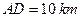 ,
,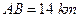 ,
,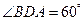 ,
,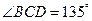 ,求两景点
,求两景点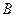 与
与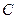 的距离(精确到0.1km).参考数据:
的距离(精确到0.1km).参考数据:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com