练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知点D(0，－2)，过点D作抛物线C1：x2＝2py(p＞0)的切线l，切点A在第二象限，如下图．

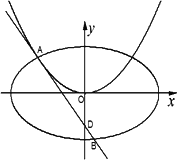
    (Ⅰ)求切点A的纵坐标；

    (Ⅱ)若离心率为的椭圆恰好经过切点A，设切线l交椭圆的另一点为B，记切线l，OA，OB的斜率分别为k，k1，k2，若k1＋2k2＝4k，求椭圆方程．

    答案：
    解析：

    　　解：(Ⅰ)设切点，且，

    　　由切线的斜率为，得的方程为，又点在上，

    　　，即点的纵坐标．

    　　(Ⅱ)由(Ⅰ)得，切线斜率，

    　　设，切线方程为，由，得，所以椭圆方程为，且过，

    　　由，

    　　，

    　　

    　　

    　　将，代入得：，所以，

    　　椭圆方程为．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （2009•黄浦区二模）已知点P（0，b）是y轴上的动点，点F（1，0）、M（a，0）满足PM⊥PF，动点N满足2
    PN
    +
    NM
    =
    0
    ．
    （1）求动点N所在曲线C的方程．
    （2）已知点D（1，2）在曲线C上，若曲线C上两点A、B（都不同于D点）满足DA⊥DB，试证明直线AB必过定点，并求出这个定点的坐标．

    查看答案和解析>>

    科目：高中数学 来源：山东省实验中学2011届高三5月针对性练习数学理综试题 题型：044

    已知点D(0，－2)，过点D作抛线C1：x2＝2py(p＞0)的切线l，切点A在第一象限，如图．

    (1)求切点A的纵坐标；

    (2)若离心率为的椭圆恰好经过切点A，设切线l交椭圆的另一点为B，记切线l，OA，OB的斜率分别为k，k1，k2，若2k1＋k2＝3k，求抛物线C1和椭圆C2的方程．

    (3)设P、Q分别是(2)中的椭圆C2的右顶点和上顶点，M是椭圆C2在第一象限的任意一点，求四边形OPMQ面积的最大值以及此时M点的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知中心在坐标原点的双曲线C的右焦点为（2，0），右顶点为（3，0）.

    （1）求双曲线C的方程；

    （2）求若直线l：y=kx+与双曲线C恒有两个不同的交点A和B，且＞2(其中O为原点)，求k的取值范围；

    （3）已知点M(,0),在（2）的条件下，求M到直线l的距离d的取值范围.

    查看答案和解析>>

    科目：高中数学 来源：2009年上海市黄浦区高考数学二模试卷（理科）（解析版） 题型：解答题

    已知点P（0，b）是y轴上的动点，点F（1，0）、M（a，0）满足PM⊥PF，动点N满足．
    （1）求动点N所在曲线C的方程．
    （2）已知点D（1，2）在曲线C上，若曲线C上两点A、B（都不同于D点）满足DA⊥DB，试证明直线AB必过定点，并求出这个定点的坐标．

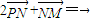    查看答案和解析>>

    同步练习册答案