
在四棱锥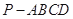 中,侧面
中,侧面
 底面
底面 ,
,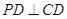 ,底面
,底面 是直角梯形,
是直角梯形,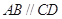 ,
,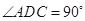 ,
,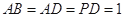 ,
, .
.
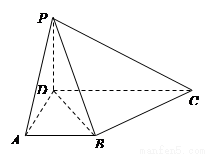
(Ⅰ)求证: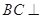 平面
平面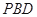 ;
;
(Ⅱ)设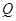 为侧棱
为侧棱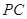 上一点,
上一点, ,试确定
,试确定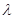 的值,使得二面角
的值,使得二面角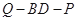 为
为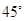 .
.
(Ⅰ)以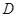 为原点建立空间直角坐标系
为原点建立空间直角坐标系 则
则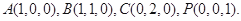
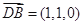 ,
,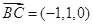 ,所以
,所以 ,
,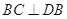 , 又由
, 又由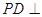 平面
平面 ,可得
,可得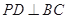 ,所以
,所以 平面
平面 .(Ⅱ)
.(Ⅱ)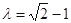
【解析】
试题分析:解法一:
(Ⅰ)平面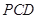
 底面
底面 ,
, ,所以
,所以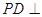 平面
平面 ,………1分
,………1分
所以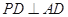 ,
.……2分
,
.……2分
如图,以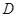 为原点建立空间直角坐标系
为原点建立空间直角坐标系 .
.

则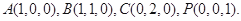 3分
3分
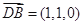 ,
,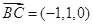 ,
,
所以 ,
,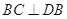 , 4分
, 4分
又由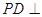 平面
平面 ,可得
,可得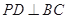 ,所以
,所以 平面
平面 . 6分
. 6分
(Ⅱ)平面 的法向量为
的法向量为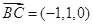 , 7分
, 7分
 ,
, ,
,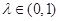
所以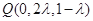 , 8分
, 8分
设平面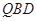 的法向量为
的法向量为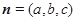 ,
,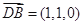 ,
, ,
,
由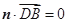 ,
,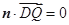 ,得
,得
所以,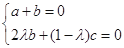 , 9分
, 9分
所以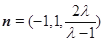 , 10分
, 10分
所以 , 11分
, 11分
注意到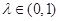 ,得
,得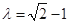 . 12分
. 12分
法二:(Ⅰ)∵面PCD⊥底面ABCD,面PCD∩底面ABCD=CD,PD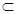 面PCD,且PD⊥CD
面PCD,且PD⊥CD
∴PD⊥面ABCD,………1分 又BC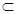 面ABCD,∴BC⊥PD ①…. .…..……2分
面ABCD,∴BC⊥PD ①…. .…..……2分
取CD中点E,连结BE,则BE⊥CD,且BE=1
在Rt△ABD中, ,在Rt△BCE中,BC=
,在Rt△BCE中,BC=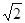 4分
4分
∵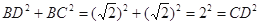 , ∴BC⊥BD ②5分
, ∴BC⊥BD ②5分
由①、②且PD∩BD=D
∴BC⊥面PBD. 6分
(Ⅱ)过Q作QF//BC交PB于F,过F作FG⊥BD于G,连结 GQ.
∵BC⊥面PBD,QF//BC
∴QF⊥面PBD,∴FG为QG在面PBD上的射影,
又∵BD⊥FG ∴BD⊥QG
∴∠FGQ为二面角Q-BD-P的平面角;由题意,∠FGQ="45°" 8分
设PQ=x,易知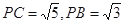
∵FQ//BC,∴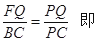

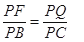
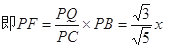
∵FG//PD∴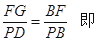
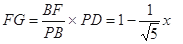 10分
10分
在Rt△FGQ中,∠FGQ=45°
∴FQ=FG,即
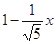 ∴
∴ … 11分
… 11分
∵ ∴
∴ ∴
∴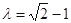 … 12分
… 12分
考点:线面垂直及二面角
点评:本题中结合已知条件可知利用空间向量法求解较简单,要证明线面垂直只需证明直线的方向向量与平面的法向量平行,二面角大小为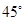 只需满足两半平面的法向量夹角为
只需满足两半平面的法向量夹角为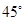


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源:2014届广东省广州市海珠区高三入学摸底考试理科数学试卷(解析版) 题型:解答题
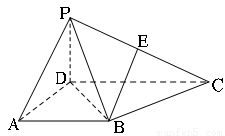
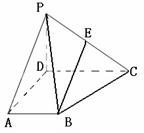
如图,在四棱锥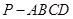 中,侧面
中,侧面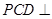 底面
底面 ,
, ,
, 为
为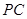 中点,底面
中点,底面 是直角梯形,
是直角梯形,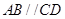 ,
,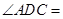
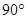 ,
,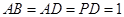 ,
,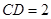 .
.
(1) 求证: 平面
平面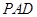 ;
;
(2) 求证:平面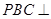 平面
平面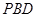 ;
;
(3) 设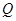 为棱
为棱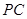 上一点,
上一点, ,试确定
,试确定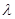 的值使得二面角
的值使得二面角 为
为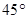 .
.
查看答案和解析>>
科目:高中数学 来源:2014届广东省“十校”高三第一次联考理科数学试卷(解析版) 题型:解答题
在四棱锥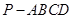 中,侧面
中,侧面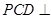 底面
底面 ,
,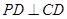 ,
,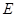 为
为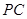 中点,底面
中点,底面 是直角梯形,
是直角梯形,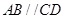 ,
,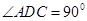 ,
, ,
,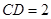 .
.
(1)求证: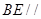 面
面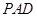 ;
;
(2)求证:面 面
面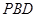 ;
;
(3)设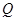 为棱
为棱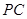 上一点,
上一点,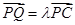 ,试确定
,试确定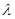 的值使得二面角
的值使得二面角 为
为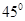 .
.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广西省高三高考模拟考试理数 题型:解答题
(本小题满分12分)(注意:在试题卷上作答无效)
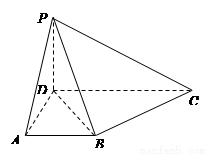
在四棱锥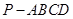 中,侧面
中,侧面
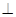 底面
底面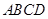 ,
,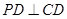 ,底面
,底面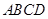 是直角梯形,
是直角梯形,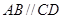 ,
,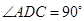 ,
,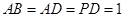 ,
,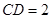 .
.
(Ⅰ)求证: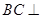 平面
平面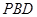 ;
;
(Ⅱ)设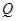 为侧棱
为侧棱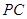 上一点,
上一点,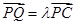 ,
,
试确定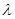 的值,使得二面角
的值,使得二面角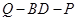 为
为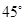 .
.
查看答案和解析>>
科目:高中数学 来源:北京市西城区2010年高三一模数学(理)试题 题型:解答题
(本小题满分14分)
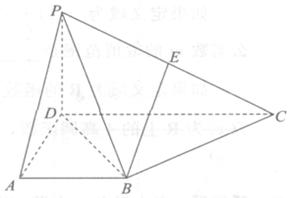
在四棱锥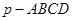 中,侧面
中,侧面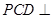 底面
底面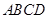 ,
,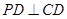 ,
,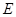 为
为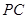 中点,底面
中点,底面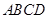 是直角梯形,
是直角梯形,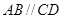 ,
,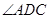 =90°,
=90°,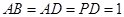 ,
,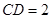 。
。
(I)求证: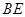
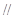 平面
平面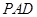 ;
;
(II)求证: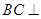 平面
平面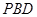 ;
;
(III)设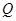 为侧棱
为侧棱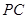 上一点,
上一点,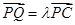 ,试确定
,试确定 的值,使得二面角
的值,使得二面角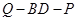 为45°。
为45°。
查看答案和解析>>
科目:高中数学 来源:2010年靖安中学高三高考模拟考试数学卷 题型:解答题
(本小题满分12分)在四棱锥 中,侧面
中,侧面 底面
底面 ,
,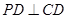 ,
, 为
为 中点,底面
中点,底面 是直角梯形,
是直角梯形,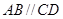 ,
, =90°,
=90°, ,
, .
.
(1)求证:
 平面
平面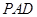 ;
;
(2)求证: 平面
平面 ;
;
(3)设 为侧棱
为侧棱 上一点,
上一点, ,
,
试确定 的值,使得二面角
的值,使得二面角 为45°.
为45°.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com