练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．当0＜x＜1时，下列不等式成立的是（　　）
    A．（$\frac{1}{2}$）x+1＞（$\frac{1}{2}$）1-xB．log（1+x）（1-x）＞1C．0＜1-x2＜1D．log（1-x）（1+x）＞0

    分析 根据指数函数，幂函数，对数函数的性质即可判断．

    解答 解：法一：考查答案A：∵0＜x＜1，∴x+1＞1-x．∴（$\frac{1}{2}$）x+1＜（$\frac{1}{2}$）1-x，故A不正确；
    考查答案B：∵0＜x＜1，∴1+x＞1，0＜1-x＜1．∴log（1+x）（1-x）＜0，故B不正确；
    考查答案C：∵0＜x＜1，∴0＜x2＜1，∴0＜1-x2＜1，故C正确；
    考查答案D：∵0＜1-x＜1，1+x＞1．∴log（1-x）（1+x）＜0．故D不正确．
    方法二：（特值法）取x=$\frac{1}{2}$，验证立得答案C．
    故选：C．

    点评 本题考查了指数函数，对数函数，幂函数的性质，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    14．已知函数f（x）=-x+log2$\frac{1-x}{1+x}$．
    （1）求函数f（x）的定义域；
    （2）当x∈[-$\frac{1}{2}$，$\frac{1}{2}$]时，求f（x）的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

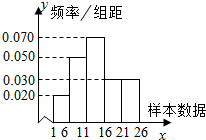    9．已知儿童退烧药，其药品安全性疑虑引起社会的广泛关注，国家药监局调查了这种的100个相关数据，绘制成如图所示的频率分布直方图，则估计样本数据的中位数为（精确到0.01）（　　）
    A．13.5B．13.14C．13.25D．13.34

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．在复平面内，复数1+i与-1+3i分别对应向量$\overrightarrow{OA}$和$\overrightarrow{OB}$，其中O为坐标原点，则$|\overrightarrow{AB}|$=$2\sqrt{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    13．已知$\overrightarrow{e}$是单位向量，向量$\overrightarrow{a}$的模为2，若$\overrightarrow{a}$=λ$\overrightarrow{e}$，则实数λ的值为±2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．不等式$\frac{x-2}{x-1}$≥2的解集是：[0，1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．数列{$\frac{2n}{n-4π}$}中的最大项是（　　）
    A．第11项B．第12项C．第13项D．第14项

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．化简：sin$\frac{4π}{3}$cos$\frac{5π}{6}$tan$\frac{3π}{4}$=-$\frac{3}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知函数f（x）=ax2-2x+1．
    （1）试讨论函数f（x）的单调性；
    （2）若$\frac{1}{3}$≤a≤1，且f（x）在[1，3]上的最大值为M（a），最小值为N（a），令g（a）=M（a）-N（a），求g（a）的表达式；
    （3）在（2）的条件下，求g（a）的最大值．

    查看答案和解析>>

    同步练习册答案