(Ⅰ)证明:∵

,N是BC的中点
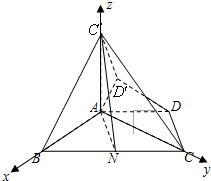
,
∴AD=NC,又AD∥BC,
∴四边形ANCD是平行四边形,∴AN=DC.
又∵等腰梯形,∴AN=AB.
又∠ABC=60°,
∴△ABN是等边三角形.
∴
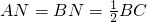
,
∴△ABC是直角三角形,且∠BAC=90°.
∴AC⊥AB.
∵平面CBA⊥平面ABC,
∴AC⊥平面ABC
′.
(Ⅱ)证明:∵AD∥BC,AD
′∥BC
′,
AD
′∩AD=A,BC∩BC
′=B,
∴平面ADD
′∥平面BCC
′,
∴C
′N∥平面ADD
′.
(Ⅲ)∵AC⊥平面ABC
′,
同理AC
′⊥平面ABC,建立如图如示坐标系
设AB=1,
则B(1,0,0),C
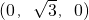
,

,
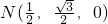
,
则
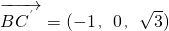
,

.
设平面C
′NC的法向量为

,
则
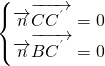
,即
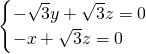
,
令z=1,则x=

,y=1,得
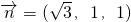
.
∵AC
′⊥平面ABC,∴平面C
′AN⊥平面ABC.
又BD⊥AN,平面C
′AN∩平面ABC=AN,
∴BD⊥平面C
′AN,
设BD与AN交于点O,O则为AN的中点,O

.
所以平面C
′AN的法向量

.
∴
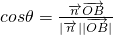
=

.
由图形可知二面角A-C
′N-C为钝角.
所以二面角A-C
′N-C的余弦值为
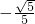
.
分析:(Ⅰ)由梯形的性质和N是BC的中点可得四边形ANCD是平行四边形,得到AN=DC;利用等腰梯形可得AN=AB,又∠ABC=60°,得到△ABN是等边三角形,于是AN=BN=NC,由出可得△ABC是直角三角形,即AC⊥AB,再利用面面垂直的性质即可得到结论;
(Ⅱ)由已知可得:AD∥BC,AD
′∥BC
′,利用面面平行的判定定理即可得出;
(Ⅲ)如图所示的空间直角坐标系,求出两个平面的法向量,利用法向量的夹角即可得到二面角的一余弦值.
点评:熟练掌握等腰梯形的性质、平行四边形的判定与性质、等边三角形及直角三角形的判定与性质、面面垂直与平行的判定及性质、通过建立空间直角坐标系利用法向量的夹角求空间角是解题的关键.

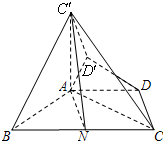 在等腰梯形ABCD中,AD∥BC,AD=
在等腰梯形ABCD中,AD∥BC,AD= BC,∠ABC=60°,N是BC的中点.将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
BC,∠ABC=60°,N是BC的中点.将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图). ,N是BC的中点
,N是BC的中点 ,
,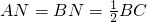 ,
,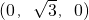 ,
, ,
,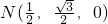 ,
,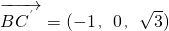 ,
, .
. ,
,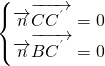 ,即
,即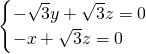 ,
, ,y=1,得
,y=1,得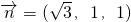 .
. .
. .
. 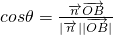 =
= .
.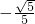 .
.

 阅读快车系列答案
阅读快车系列答案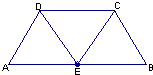 如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥P-DCE的外接球的体积为
如图,在等腰梯形ABCD中,AB=2DC=2,∠DAB=60°,E为AB的中点,将△ADE与△BEC分别沿ED、EC向上折起,使A、B重合于点P,则三棱锥P-DCE的外接球的体积为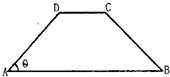 如图,在等腰梯形ABCD中,AB∥CD,且AB=2AD,设∠DAB=θ,θ∈(0,
如图,在等腰梯形ABCD中,AB∥CD,且AB=2AD,设∠DAB=θ,θ∈(0, 在等腰梯形ABCD中,E、F分别是CD、AB中点,CD=2,AB=4,AD=BC=
在等腰梯形ABCD中,E、F分别是CD、AB中点,CD=2,AB=4,AD=BC= 如图,在等腰梯形ABCD中,M,N分别是AB,CD的中点,沿MN将MNCB折起至MNC1B1,使它与MNDA成直二面角.已知AB=2CD=4MN,给出下列四个等式:
如图,在等腰梯形ABCD中,M,N分别是AB,CD的中点,沿MN将MNCB折起至MNC1B1,使它与MNDA成直二面角.已知AB=2CD=4MN,给出下列四个等式: 如图,在等腰梯形ABCD中,AB=6,CD=4,梯形ABCD的面积是5
如图,在等腰梯形ABCD中,AB=6,CD=4,梯形ABCD的面积是5