
| 2 |
| d |
| |r| |
| 2 |
| |3-r| | ||
|
| d |
| |r| |
| 2 |


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
 如图是一幅招贴画的示意图,其中ABCD是边长为2a的正方形,周围是四个全等的弓形.已知O为正方形的中心,G为AD的中点,点P在直线OG上,弧AD是以P为圆心、PA为半径的圆的一部分,OG的延长线交弧AD于点H.设弧AD的长为l,∠APH=θ,θ∈(
如图是一幅招贴画的示意图,其中ABCD是边长为2a的正方形,周围是四个全等的弓形.已知O为正方形的中心,G为AD的中点,点P在直线OG上,弧AD是以P为圆心、PA为半径的圆的一部分,OG的延长线交弧AD于点H.设弧AD的长为l,∠APH=θ,θ∈(| π |
| 4 |
| 3π |
| 4 |
| OP |
| l |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源:江苏期末题 题型:解答题
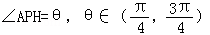 .
.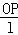 为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角θ满足:
为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角θ满足: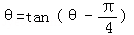 时,招贴画最优美.
时,招贴画最优美.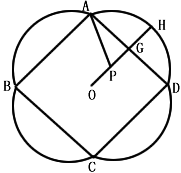
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012年江苏省常州市教育学会高三1月学业水平监测数学试题(解析版) 题型:解答题
 .(1)求l关于θ的函数关系式;(2)定义比值
.(1)求l关于θ的函数关系式;(2)定义比值 为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角θ满足:
为招贴画的优美系数,当优美系数最大时,招贴画最优美.证明:当角θ满足: 时,招贴画最优美.
时,招贴画最优美.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com