
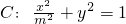 (常数m>1),P是曲线C上的动点,M是曲线C上的右顶点,定点A的坐标为(2,0)
(常数m>1),P是曲线C上的动点,M是曲线C上的右顶点,定点A的坐标为(2,0) ;
; ,0),(-
,0),(- ,0);
,0); +y2=1;
+y2=1; ,
,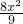 -4x+5;
-4x+5;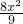 -4x+5取得最大值,且最大值为25;
-4x+5取得最大值,且最大值为25; 时,|PA|2=
时,|PA|2=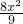 -4x+5取得最小值,且最小值为
-4x+5取得最小值,且最小值为 ;
; ;
; (x-
(x-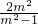 )2+
)2+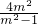 +5,且-m≤x≤m;
+5,且-m≤x≤m; >0,
>0,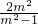 ≥m,且m>1;
≥m,且m>1; .
. ;而|PA|2=(x-2)2+y2,将y2=1-
;而|PA|2=(x-2)2+y2,将y2=1- 代入可得,|PA|2=
代入可得,|PA|2=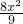 -4x+5,根据二次函数的性质,又由x的范围,分析可得,|PA|2的最大与最小值;进而可得答案;
-4x+5,根据二次函数的性质,又由x的范围,分析可得,|PA|2的最大与最小值;进而可得答案; (x-
(x-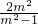 )2+
)2+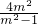 +5,且-m≤x≤m;根据题意,|PA|的最小值为|MA|,即当x=m时,|PA|取得最小值,根据二次函数的性质,分析可得,
+5,且-m≤x≤m;根据题意,|PA|的最小值为|MA|,即当x=m时,|PA|取得最小值,根据二次函数的性质,分析可得,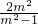 ≥m,且m>1;解可得答案.
≥m,且m>1;解可得答案.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2012-2013学年云南师大附中高考适应性月考数学试卷4(文科)(解析版) 题型:解答题
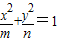 (常数m、n∈R+,且m>n)的左右焦点分别为F1,F2 ,M、N为短轴的两个端点,且四边形F1MF2N是边长为2的正方形.
(常数m、n∈R+,且m>n)的左右焦点分别为F1,F2 ,M、N为短轴的两个端点,且四边形F1MF2N是边长为2的正方形.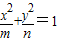 的交点为A、B、C、D(按逆时针顺序排列,且点A位于第一象限内),求四边形ABCD的面积S的最大值..
的交点为A、B、C、D(按逆时针顺序排列,且点A位于第一象限内),求四边形ABCD的面积S的最大值..查看答案和解析>>
科目:高中数学 来源:2012-2013学年云南师大附中高考适应性月考数学试卷4(文科)(解析版) 题型:解答题
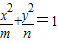 (常数m、n∈R+,且m>n)的左右焦点分别为F1,F2 ,M、N为短轴的两个端点,且四边形F1MF2N是边长为2的正方形.
(常数m、n∈R+,且m>n)的左右焦点分别为F1,F2 ,M、N为短轴的两个端点,且四边形F1MF2N是边长为2的正方形.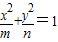 的交点为A、B、C、D(按逆时针顺序排列,且点A位于第一象限内),求四边形ABCD的面积S的最大值..
的交点为A、B、C、D(按逆时针顺序排列,且点A位于第一象限内),求四边形ABCD的面积S的最大值..查看答案和解析>>
科目:高中数学 来源:2010-2011学年吉林省长春外国语学校高二(下)期末数学试卷(文科)(解析版) 题型:解答题
 (常数m>1),P是曲线C上的动点,M是曲线C上的右顶点,定点A的坐标为(2,0)
(常数m>1),P是曲线C上的动点,M是曲线C上的右顶点,定点A的坐标为(2,0)查看答案和解析>>
科目:高中数学 来源:2010年上海市嘉定区、黄浦区高考数学二模试卷(理科)(解析版) 题型:解答题
 ,常数m、n∈R+,且m>n.
,常数m、n∈R+,且m>n. ,求直线PQ的斜率;
,求直线PQ的斜率; 的交点为A、B、C、D(按逆时针顺序排列,且点A位于第一象限内),试用k表示四边形ABCD的面积S;
的交点为A、B、C、D(按逆时针顺序排列,且点A位于第一象限内),试用k表示四边形ABCD的面积S;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com