
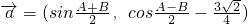 ,
,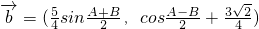 ,其中A、B是△ABC的内角,
,其中A、B是△ABC的内角, ⊥
⊥ ,
, •
• =
= sin2
sin2 +(cos2
+(cos2 -
- )=
)= [1-cos(A+B)]+
[1-cos(A+B)]+ [1+cos(A-B)]-
[1+cos(A-B)]-
 cos(A-B)-
cos(A-B)- cos(A+B)=
cos(A+B)= (cosAcosB+sinAsinB)-
(cosAcosB+sinAsinB)- (cosAcosB-sinAsinB)
(cosAcosB-sinAsinB) sinAsinB-
sinAsinB- cosAcosB
cosAcosB ⊥
⊥ ,
, •
• =0,即
=0,即 sinAsinB-
sinAsinB- cosAcosB=0,可得sinAsinB=
cosAcosB=0,可得sinAsinB= cosAcosB
cosAcosB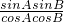 =
=
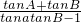 =-
=- (tanA+tanB)
(tanA+tanB)  >0
>0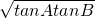 =
=
 (tanA+tanB)≤-
(tanA+tanB)≤- ×
× =-
=- ,即tanC≤-
,即tanC≤- ,
, 时,tanC的最大值为-
时,tanC的最大值为- .
. •
• 展开,并用三角函数的降幂公式、和与差的余弦公式化简得:
展开,并用三角函数的降幂公式、和与差的余弦公式化简得: •
• =
= sinAsinB-
sinAsinB- cosAcosB,再由
cosAcosB,再由 ⊥
⊥ ,得到
,得到 sinAsinB-
sinAsinB- cosAcosB=0,最后可用同角三角函数的商数关系,得到tanAtanB=
cosAcosB=0,最后可用同角三角函数的商数关系,得到tanAtanB= ;
; (tanA+tanB),再经过讨论可得tanA、tanB都是正数,所以tanA+tanB≥2
(tanA+tanB),再经过讨论可得tanA、tanB都是正数,所以tanA+tanB≥2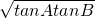 =
= ,从而得到当且仅当tanA=tanB=
,从而得到当且仅当tanA=tanB= 时,tanC的最大值为-
时,tanC的最大值为- .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2011-2012学年江西省吉安市安福中学高三(上)第一次月考数学试卷(文科)(解析版) 题型:解答题
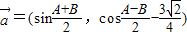 ,
,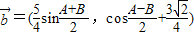 ,其中A、B是△ABC的内角,
,其中A、B是△ABC的内角,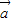 ⊥
⊥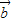 ,
,查看答案和解析>>
科目:高中数学 来源:2013年吉林省吉林一中高考数学模拟试卷(一)(解析版) 题型:解答题
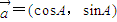 ,
,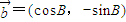 ,其中∠A,∠B为△ABC的内角,且
,其中∠A,∠B为△ABC的内角,且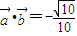 .
. .
.查看答案和解析>>
科目:高中数学 来源:2011年四川省南充市高考数学零诊试卷(文科)(解析版) 题型:选择题
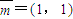 ,
,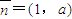 ,其中a为实数,当
,其中a为实数,当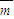 与
与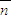 的夹角在区间
的夹角在区间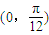 范围内变动时,实数a的取值范围是( )
范围内变动时,实数a的取值范围是( ) ,
,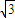 )
)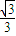 ,1)
,1)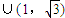
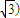
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com