
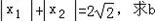 的最大值;
的最大值;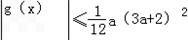 .
.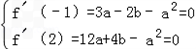 ,(a>0)
,(a>0)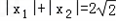 ,
,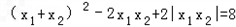 ,
,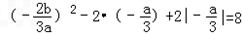 ,
,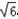
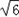 .
.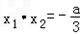 ,x2=a,
,x2=a,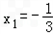 ,
, )[3(x﹣a)﹣1],
)[3(x﹣a)﹣1],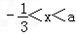 ,
,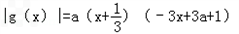 ,
,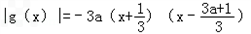 =﹣3a
=﹣3a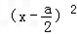 +
+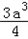 +
+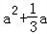
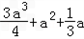 =
=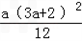 ,
,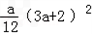 成立.
成立.

 特高级教师点拨系列答案
特高级教师点拨系列答案科目:高中数学 来源: 题型:
| a | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| f(x1)-f(x2) |
| x1-x2 |
| f(x1)-f(x2) |
| x1-x2 |
查看答案和解析>>
科目:高中数学 来源:广东省2007年五校联考调研数学试卷(理科)-苏教版 题型:044
设x1,x2是![]() 的两个极值点,f(x)的导函数是
的两个极值点,f(x)的导函数是![]()
(1)如果x1<2<x2<4,求证:![]() ;
;
(2)如果|x1|<2,|x2-x1|=2,求b的取值范围;
(3)如果a≥2,且x2-x1=2,x∈(x1,x2)时,函数![]() 的最小值为h(a),求h(a)的最大值.
的最小值为h(a),求h(a)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
①f(x1)f(-x1)≤0 ②f(x2)f(-x2)>0 ③f(x1)+f(x2)≤f(-x1)+f(-x2)④f(x1)+f(x2)≥f(-x1)+f(-x2)
A.①③ B.①④ C.②③ D.②④
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| f(x1)-f(x2) |
| x1-x2 |
| f(x1)-f(x2) |
| x1-x2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com