
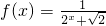 ,利用课本中推导等差数列前n项和公式的方法,可求得f(-5)+f(-4)+…+f(0)+…+f(5)+f(6)的值是________.
,利用课本中推导等差数列前n项和公式的方法,可求得f(-5)+f(-4)+…+f(0)+…+f(5)+f(6)的值是________. 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:填空题
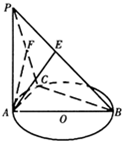 如图,AB是⊙O的直径,C是圆周上不同于A、B的点,PA垂直于⊙O所在平面AE⊥PB于E,AF⊥PC于F,因此________⊥平面PBC(请填图上的一条直线)
如图,AB是⊙O的直径,C是圆周上不同于A、B的点,PA垂直于⊙O所在平面AE⊥PB于E,AF⊥PC于F,因此________⊥平面PBC(请填图上的一条直线)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
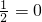 有两个不等的实数根.若“p∧q”为假命题,“p∨q”为真命题,求a的取值范围.
有两个不等的实数根.若“p∧q”为假命题,“p∨q”为真命题,求a的取值范围.查看答案和解析>>
科目:高中数学 来源: 题型:单选题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 )<f(cos
)<f(cos )
) )<f(sin
)<f(sin )
)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 ,圆O:x2+y2=5,椭圆E:
,圆O:x2+y2=5,椭圆E: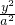 +
+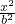 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= .直线l截圆O所得的弦长与椭圆的短轴长相等.
.直线l截圆O所得的弦长与椭圆的短轴长相等.查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 x2
x2查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com