设{an}和{bn}均为无穷数列.
(1)若{an}和{bn}均为等比数列,试研究:{an+bn}和{anbn}是否是等比数列?请证明你的结论;若是等比数列,请写出其前n项和公式.
(2)请类比(1),针对等差数列提出相应的真命题(不必证明),并写出相应的等差数列的前n项和公式(用首项与公差表示).
【答案】
分析:(1)讨论两数列的公比,根据等比数列的性质可判定{a
n+b
n}和{a
nb
n}是否是等比数列,然后利用等比数列的求和公式解之即可;
(2)利用等比中的乘类比到等差中的和,讨论公差是否为0,从而求出相应的等差数列的前n项和公式.
解答:解:(1)①设c
n=a
n+b
n,
则

-(
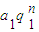
+
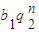
)(
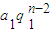
+
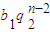
)
=a
1b
1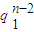
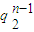
(q
1-q
2)2
当q
1=q
2时,对任意的n∈N,n≥2,

=c
n+1c
n-1恒成立,
故{a
n+b
n}为等比数列; (3分)
∴S
n=
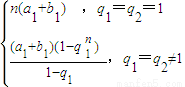
(1分)
当q
1≠q
2时,
对任意的n∈N,n≥2,

≠c
n+1c
n-1,{a
n+b
n}不是等比数列.(2分)
②设d
n=a
nb
n,
对于任意n∈N
*,
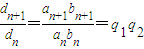
,{a
nb
n}是等比数列. (3分)
S
n=
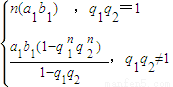
(1分)
(2)设{a
n},{b
n}均为等差数列,公差分别为d
1,d
2,则:
①{a
n+b
n}为等差数列;S
n=(a
1+b
1)n+
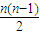
(d
1+d
2)(2分)
②当d
1与d
2至少有一个为0时,{a
nb
n}是等差数列,(1分)
若d
1=0,S
n=a
1b
1n+
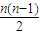
a
1d
2;(1分)
若d
2=0,S
n=a
1b
1n+
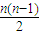
b
1d
1.(1分)
③当d
1与d
2都不为0时,{a
nb
n}一定不是等差数列.(1分)
点评:本题主要考查了类比推理,以及等比数列与等差数列的判定,同时考查了计算能力和分析求解的能力,属于基础题.

 -(
-(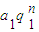 +
+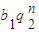 )(
)(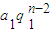 +
+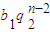 )
)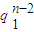
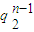 (q1-q2)2
(q1-q2)2 =cn+1cn-1恒成立,
=cn+1cn-1恒成立,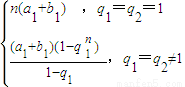 (1分)
(1分) ≠cn+1cn-1,{an+bn}不是等比数列.(2分)
≠cn+1cn-1,{an+bn}不是等比数列.(2分)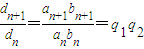 ,{anbn}是等比数列. (3分)
,{anbn}是等比数列. (3分)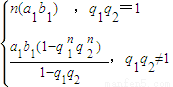 (1分)
(1分)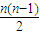 (d1+d2)(2分)
(d1+d2)(2分)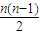 a1d2;(1分)
a1d2;(1分)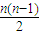 b1d1.(1分)
b1d1.(1分)

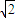 ,|β|>2
,|β|>2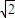
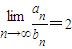 ,则
,则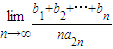 的值为 .
的值为 .