
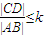 ,其中k为常数,且0<k<1,求S的最大值.
,其中k为常数,且0<k<1,求S的最大值.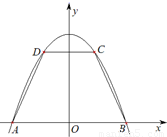
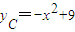 .…(1分)
.…(1分)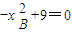 ,解得xB=3,舍去xB=-3. …(2分)
,解得xB=3,舍去xB=-3. …(2分)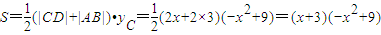 .…(4分)
.…(4分)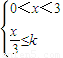 及0<k<1,得0<x≤3k. …(6分)
及0<k<1,得0<x≤3k. …(6分)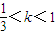 时,f'(x)与f(x)的变化情况如下:
时,f'(x)与f(x)的变化情况如下:| x | (0,1) | 1 | (1,3k) |
| f'(x) | + | - | |
| f(x) | ↗ | 极大值 | ↘ |
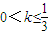 时,f'(x)>0恒成立,
时,f'(x)>0恒成立,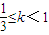 时,S的最大值为32;
时,S的最大值为32;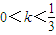 时,S的最大值为27(1+k)(1-k2).
时,S的最大值为27(1+k)(1-k2).

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
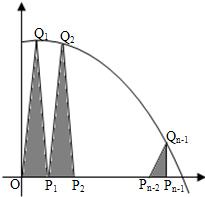 如图,抛物线y=-x2+1与x轴的正半轴交于点A,将线段OA的n等分点从左至右依次记为P1,P2,…,Pn-1,过这些分点分别作x轴的垂线,与抛物线的交点依次为Q1,Q2,…,Qn-1,从而得到n-1个直角三角形△Q1OP1,△Q2P1P2,…,△Qn-1Pn-2Pn-1.当n→∞时,这些三角形的面积之和的极限为
如图,抛物线y=-x2+1与x轴的正半轴交于点A,将线段OA的n等分点从左至右依次记为P1,P2,…,Pn-1,过这些分点分别作x轴的垂线,与抛物线的交点依次为Q1,Q2,…,Qn-1,从而得到n-1个直角三角形△Q1OP1,△Q2P1P2,…,△Qn-1Pn-2Pn-1.当n→∞时,这些三角形的面积之和的极限为查看答案和解析>>
科目:高中数学 来源: 题型:
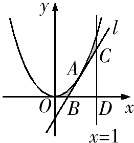 如图,抛物线y=x2上有一点A(a,a2),a∈(0,1),过点A引抛物线的切线l分别交x轴与直线x=1于B,C两点,直线x=1交x轴于点D.
如图,抛物线y=x2上有一点A(a,a2),a∈(0,1),过点A引抛物线的切线l分别交x轴与直线x=1于B,C两点,直线x=1交x轴于点D.查看答案和解析>>
科目:高中数学 来源: 题型:
 已知如图,抛物线y=ax2+bx+2与x轴的交点是A(3,0)、B(6,0),与y轴的交点是C.
已知如图,抛物线y=ax2+bx+2与x轴的交点是A(3,0)、B(6,0),与y轴的交点是C.查看答案和解析>>
科目:高中数学 来源: 题型:
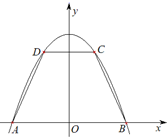 (2012•西城区一模)如图,抛物线y=-x2+9与x轴交于两点A,B,点C,D在抛物线上(点C在第一象限),CD∥AB.记|CD|=2x,梯形ABCD面积为S.
(2012•西城区一模)如图,抛物线y=-x2+9与x轴交于两点A,B,点C,D在抛物线上(点C在第一象限),CD∥AB.记|CD|=2x,梯形ABCD面积为S.| |CD| | |AB| |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.
如图,抛物线y=ax2-5ax+4经过△ABC的三个顶点,已知BC∥x轴,点A在x轴上,点C在y轴上,且AC=BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com