
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 黄瓜 | 4吨 | 1.2万元 | 0.55万元 |
| 韭菜 | 6吨 | 0.9万元 | 0.3万元 |
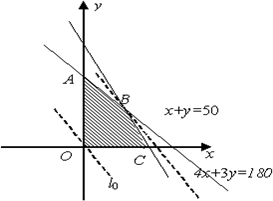 解:设黄瓜和韭菜的种植面积分别为x,y亩,总利润为z万元,
解:设黄瓜和韭菜的种植面积分别为x,y亩,总利润为z万元,
|
|
|


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源: 题型:
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、方程f(x)=k(k∈R)有且仅有一个解 |
| B、函数f(x)的最大值为1 |
| C、函数f(x)是增函数 |
| D、函数f(x)的最小值为0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| S(n+1) |
| Sn |
| Sn•S(n+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:
 某天甲、乙两同学约好在晚上8点到9点之间在某地会面,假定两人到达指定地点的时刻是等可能的且相互独立的,并约定先到者等待后到者时间是15分钟,之后就可以离去,问两人能够见面的概率有多大?
某天甲、乙两同学约好在晚上8点到9点之间在某地会面,假定两人到达指定地点的时刻是等可能的且相互独立的,并约定先到者等待后到者时间是15分钟,之后就可以离去,问两人能够见面的概率有多大?查看答案和解析>>
科目:高中数学 来源: 题型:
A、(0,
| ||||
B、(0,
| ||||
C、[
| ||||
D、(
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com