
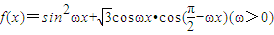 ,且函数y=f(x)的图象相邻两条对称轴之间的距离为
,且函数y=f(x)的图象相邻两条对称轴之间的距离为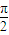 .
.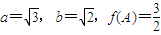 ,求角C.
,求角C.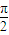 ,2kπ+
,2kπ+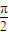 ]即可得到函数的单调递增区间;
]即可得到函数的单调递增区间; ,再根据A为三角形的内角,利用特殊角的三角函数值求出A的度数,然后由a,sinA与b的值,利用正弦定理求出sinB的值,由B为三角形的内角,且根据b小于a,利用三角形的边角关系得到B为锐角,利用特殊角的三角函数值求出B的度数,进而利用三角形的内角和定理求出C的度数.
,再根据A为三角形的内角,利用特殊角的三角函数值求出A的度数,然后由a,sinA与b的值,利用正弦定理求出sinB的值,由B为三角形的内角,且根据b小于a,利用三角形的边角关系得到B为锐角,利用特殊角的三角函数值求出B的度数,进而利用三角形的内角和定理求出C的度数.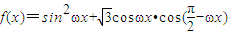
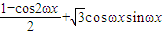
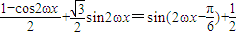 ,
,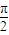 ,
,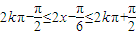 ,∴
,∴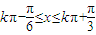 ,
,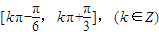 ;…(7分)
;…(7分) ,∴
,∴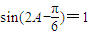 ,
,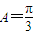 ,…(10分)
,…(10分)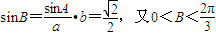 ,
,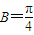 ,
,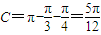 .…(14分)
.…(14分)

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
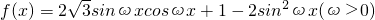 ,且函数f(x)的最小正周期为π.
,且函数f(x)的最小正周期为π.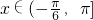 ,求函数f(x)的单调递减区间;
,求函数f(x)的单调递减区间; ,把所得到的图象再向左平移
,把所得到的图象再向左平移 个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间
个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间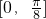 上的最小值.
上的最小值.查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省厦门外国语学校高三(上)期中数学试卷(文科)(解析版) 题型:解答题
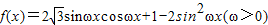 ,且函数f(x)的最小正周期为π.
,且函数f(x)的最小正周期为π.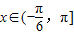 ,求函数f(x)的单调递减区间;
,求函数f(x)的单调递减区间; ,把所得到的图象再向左平移
,把所得到的图象再向左平移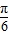 个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间
个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间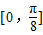 上的最小值.
上的最小值.查看答案和解析>>
科目:高中数学 来源:2011-2012学年山西省高三(上)第二次段考数学试卷(理科)(解析版) 题型:解答题
 ,且函数f(x)的最小正周期为π.
,且函数f(x)的最小正周期为π. ,求函数f(x)的单调递减区间;
,求函数f(x)的单调递减区间; ,把所得到的图象再向左平移
,把所得到的图象再向左平移 个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间
个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间 上的最小值.
上的最小值.查看答案和解析>>
科目:高中数学 来源:2011-2012学年山西省高三(上)第二次段考数学试卷(文科)(解析版) 题型:解答题
 ,且函数f(x)的最小正周期为π.
,且函数f(x)的最小正周期为π.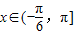 ,求函数f(x)的单调递减区间;
,求函数f(x)的单调递减区间; ,把所得到的图象再向左平移
,把所得到的图象再向左平移 个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间
个单位,得到函数y=g(x)的图象,求函数y=g(x)在区间 上的最小值.
上的最小值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com