
已知函数 ,设曲线
,设曲线 在点
在点 处的切线与
处的切线与 轴的交点为
轴的交点为 ,其中
,其中 为正实数.
为正实数.
(1)用 表示
表示 ;
;
(2) ,若
,若 ,试证明数列
,试证明数列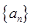 为等比数列,并求数列
为等比数列,并求数列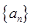 的通项公式;
的通项公式;
(3)若数列 的前
的前 项和
项和 ,记数列
,记数列 的前
的前 项和
项和 ,求
,求 .
.
(1) ;(2)证明见解析,
;(2)证明见解析, ;(3)
;(3) .
.
【解析】
试题分析:(1)直接利用导数得出切线斜率,写出点 处切线方程,在切线方程中令
处切线方程,在切线方程中令 ,就可求出切线与
,就可求出切线与 轴交点的横坐标即
轴交点的横坐标即 ;(2)要证明数列
;(2)要证明数列 为等比数列,关键是找到
为等比数列,关键是找到 与
与 的关系,按题设,它们由
的关系,按题设,它们由 联系起来,
联系起来, ,把
,把 用(1)中的结论
用(1)中的结论 代换,变为
代换,变为 的式子,它应该与
的式子,它应该与 是有联系的,由此就可得出结论;(3)按照要求,首先求出数列
是有联系的,由此就可得出结论;(3)按照要求,首先求出数列 的通项公式,当然要利用
的通项公式,当然要利用 (
( ),
), 直接等于
直接等于 ,数列
,数列 实际上是一个等差数列,那么数列
实际上是一个等差数列,那么数列 就是由一个等差数列和一个等比数列的对应项相乘得到的新数列,其前
就是由一个等差数列和一个等比数列的对应项相乘得到的新数列,其前 项的求法是乘公比错位相减法,即
项的求法是乘公比错位相减法,即 ,记等比数列
,记等比数列 的公比是
的公比是 ,则有
,则有
 ,两式相减,即
,两式相减,即 ,这个和是容易求得的.
,这个和是容易求得的.
试题解析:(1)由题可得 ,所以在曲线上点
,所以在曲线上点 处的切线方程为
处的切线方程为 ,即
,即
令 ,得
,得 ,即
,即
由题意得 ,所以
,所以 5′
5′
(2)因为 ,所以
,所以
 即
即 ,
,
所以数列 为等比数列故
为等比数列故 10′
10′
(3)当 时,
时, ,当
,当 时,
时,
所以数列 的通项公式为
的通项公式为 ,故数列
,故数列 的通项公式为
的通项公式为
 ①
①
① 的
的 ②
②
① ②得
②得
故 16′
16′
考点:(1)函数图象的切线;(2)等比数列的定义;(3)乘公比错位相减法求数列的和.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源: 题型:
(07年四川卷理)(12分)已知函数![]() ,设曲线
,设曲线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴的交点为
轴的交点为![]()
![]() ,其中
,其中![]() 为正实数.
为正实数.
(Ⅰ)用![]() 表示
表示![]() ;
;
(Ⅱ) 证明:对一切正整数![]() 的充要条件是
的充要条件是![]()
(Ⅲ)若![]() ,记
,记![]() ,证明数列
,证明数列![]() 成等比数列,并求数列
成等比数列,并求数列![]() 的通项公式。
的通项公式。
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江苏省高三12月月考文科数学试卷(解析版) 题型:解答题
已知函数 ,设曲线
,设曲线 在点
在点 处的切线与
处的切线与 轴的交点为
轴的交点为 ,其中
,其中 为正实数.
为正实数.
(1)用 表示
表示 ;
;
(2) ,若
,若 ,试证明数列
,试证明数列 为等比数列,并求数列
为等比数列,并求数列 的通项公式;
的通项公式;
(3)若数列 的前
的前 项和
项和 ,记数列
,记数列 的前
的前 项和
项和 ,求
,求 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com