Question

如图,四边形ABCD是直角梯形,AB∥CD,∠ADC=∠DAB=90°,CD=2AB,PA⊥平面ABCD,PA=AB=AD=1,Q是PC的中点.

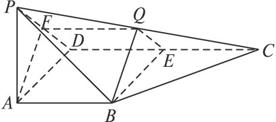
（1）求证:BQ∥平面PAD;

（2）如果点E是线段CD中点,求三棱锥Q—BEC的体积.

Answer 1

(1)证明:取PD的中点F,连结AF、FQ，

∵Q为PC的中点,则FQ为△PCD的中位线.

∴FQ∥CD且FQ=CD.

又∵AB∥CD且AB=CD,∴FQ∥AB且FQ=AB.

∴四边形ABQF为平行四边形,BQ∥AF.

又∵AF在平面PAD内,BQ在平面PAD外,∴BQ∥平面PAD.

(2)解法一:∵当E为CD的中点时,则DE∥AB且DE=AB,∴四边形ABED为平行四边形.

∴BE∥AD.又∠ADC=90°，∴CE⊥BE.

又∵PA⊥平面ABCD，CD在平面ABCD内，∴PA⊥CD.又CD⊥AD，∴CD⊥面PAD，CD⊥PD.∵QE∥PD，∴CE⊥QE.∴CE⊥平面BQE.

∵在△PAD中,AD=AP,F为PD的中点,∴AF⊥PD.又∵AF面PAD,∴AF⊥CD.

又PD∩CD=D,∴AF⊥面PCD.由BQ∥AF得BQ⊥面PCD,∴BQ⊥QE.

V_Q—BCE=V_C—BQE=CE·S_△BQE=·1···=.

解法二：∵PA⊥面ABCD，∴点Q在面ABCD内的射影在AC上.

设Q到平面ABCD的距离为h，则h=PA=.

V_Q—BCE=h·S_△BQE=··CE·BE=.