
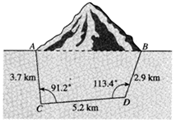
 工程队将从A到B修建一条隧道,测量员测得图中的一些数据(A、B、C、D在同一水平面内),求A、B之间的距离.
工程队将从A到B修建一条隧道,测量员测得图中的一些数据(A、B、C、D在同一水平面内),求A、B之间的距离. 解:连结AD,在△ACD中,由余弦定理可得
解:连结AD,在△ACD中,由余弦定理可得| ACsin91.2° |
| AD |


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com