ABC中,A(0,1),AB边上的高线方程为x+2y-4=0,AC边上的中线方程为2x+y-3=0,求AB,BC,AC边所在的直线方程.
分析:先找出AB边上的高线方程的斜率,根据两直线垂直时斜率乘积为-1求出直线AB的斜率和A的坐标,即可写出直线AB的方程;把直线AB与AC边上的中线方程联立求出交点B的坐标,然后设出AC的中点D和C的坐标,根据中点坐标公式列出方程组,求出解即可得到C的坐标,利用两点坐标写出直线BC的方程;由A和C的坐标写出直线AC的方程即可.
解答:解:AB边上的高线方程为x+2y-4=0得到高线的方程斜率为-
,则直线AB的斜率为2,又过A(0,1)
∴AB边所在的直线方程为:y-1=2(x-0)化简得2x-y+1=0;
联立直线AB与AC边中线的方程
,解得
,所以交点
B(,2),
设AC边中点D(x
1,3-2x
1),C(4-2y
1,y
1),
∵D为AC的中点,由中点坐标公式得
解得y
1=1,
∴C(2,1)
∴BC直线方程为y-1=
(x-2),化简得2x+3y-7=0;
AC边所在的直线方程为y-1=
(x-0),化简得y=1.
点评:考查学生掌握两直线垂直时斜率之间的关系,会根据斜率和一点坐标写出直线的方程及会根据两点坐标写出直线的方程.灵活运用两点间的距离公式化简求值.是一道综合题.



 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案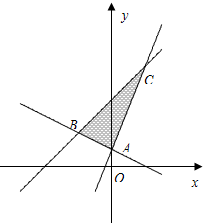 如图△ABC中,A(0,1),B(-2,2),C(2,6).
如图△ABC中,A(0,1),B(-2,2),C(2,6).