
ΓΨΧβΡΩΓΩΡ≥≤ΆΧϋΆ®Ιΐ≤ι‘ΡΝΥΉνΫϋ5¥Έ ≥ΤΖΫΜ“ΉΜα≤ΈΜα»Υ ΐ![]() (Άρ»Υ)”κ≤ΆΧϋΥυ”Ο‘≠≤ΡΝœ ΐΝΩ
(Άρ»Υ)”κ≤ΆΧϋΥυ”Ο‘≠≤ΡΝœ ΐΝΩ![]() (¥ϋ)Θ§ΒΟΒΫ»γœ¬Ά≥ΦΤ±μΘΚ
(¥ϋ)Θ§ΒΟΒΫ»γœ¬Ά≥ΦΤ±μΘΚ
ΒΎ“Μ¥Έ | ΒΎΕΰ¥Έ | ΒΎ»ΐ¥Έ | ΒΎΥΡ¥Έ | ΒΎΈε¥Έ | |
≤ΈΜα»Υ ΐ | 13 | 9 | 8 | 10 | 12 |
‘≠≤ΡΝœ | 32 | 23 | 18 | 24 | 28 |
Θ®1Θ©ΗυΨίΥυΗχ5Ήι ΐΨίΘ§«σ≥ω![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡœΏ–‘ΜΊΙιΖΫ≥Χ
ΒΡœΏ–‘ΜΊΙιΖΫ≥Χ![]() .
.
Θ®2Θ©“―÷ΣΙΚ¬ρ‘≠≤ΡΝœΒΡΖ―”Ο![]() (‘Σ)”κ ΐΝΩ
(‘Σ)”κ ΐΝΩ![]() (¥ϋ)ΒΡΙΊœΒΈΣ
(¥ϋ)ΒΡΙΊœΒΈΣ![]() Θ§
Θ§
ΆΕ»κ Ι”ΟΒΡΟΩ¥ϋ‘≠≤ΡΝœœύ”ΠΒΡœζ έ ’»κΈΣ700‘ΣΘ§Εύ”ύΒΡ‘≠≤ΡΝœ÷ΜΡήΈό≥ΞΖΒΜΙΘ§ΨίœΛ±Ψ¥ΈΫΜ“Ή¥σΜα¥σ‘Φ”–15Άρ»Υ≤ΈΦ”Θ§ΗυΨί(1)÷–«σ≥ωΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΘ§‘Λ≤β≤ΆΧϋ”ΠΙΚ¬ρΕύ…Ό¥ϋ‘≠≤ΡΝœΘ§≤≈ΡήΜώΒΟΉν¥σάϊ»σΘ§Ήν¥σάϊ»σ «Εύ…ΌΘΩ(ΉΔΘΚάϊ»σ![]() œζ έ ’»κ
œζ έ ’»κ![]() ‘≠≤ΡΝœΖ―”Ο).
‘≠≤ΡΝœΖ―”Ο).
≤ΈΩΦΙΪ ΫΘΚ  Θ§
Θ§ ![]() .
.
≤ΈΩΦ ΐΨίΘΚ ![]() Θ§
Θ§ ![]() Θ§
Θ§ ![]() .
.
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©≤ΆΧϋ”ΠΗΟΙΚ¬ρ36¥ϋ‘≠≤ΡΝœΘ§≤≈Ρή Ιάϊ»σΜώΒΟΉν¥σΘ§Ήν¥σάϊ»σΈΣ11870‘Σ.
ΘΜΘ®2Θ©≤ΆΧϋ”ΠΗΟΙΚ¬ρ36¥ϋ‘≠≤ΡΝœΘ§≤≈Ρή Ιάϊ»σΜώΒΟΉν¥σΘ§Ήν¥σάϊ»σΈΣ11870‘Σ.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©ΗυΨίΙΪ Ϋ«σ≥ωbΘ§‘ΌΫΪ―υ±Ψ÷––Ρ¥ζ»κ«σ≥ωaΘ§ΫχΕχΒΟΒΫΜΊΙιΖΫ≥ΧΘΜΘ®2Θ©![]() Θ§άϊ»σΈΣΉ§ΒΡ«°Φθ»ΞΜ®≥ω»ΞΒΡ«°Θ§ΗυΨίΖ÷ΕΈΚ· ΐΒΡ±μ¥ο ΫΘ§Ζ÷ΕΈΝ–≥ωάϊ»σ±μ¥ο ΫΘ§Ζ÷±πΧ÷¬έάϊ»σΒΡΉν÷ΒΘ§Ήν÷’»ΓΖ÷ΕΈΚ· ΐ÷–Ϋœ¥σΒΡάϊ»σ÷Β.
Θ§άϊ»σΈΣΉ§ΒΡ«°Φθ»ΞΜ®≥ω»ΞΒΡ«°Θ§ΗυΨίΖ÷ΕΈΚ· ΐΒΡ±μ¥ο ΫΘ§Ζ÷ΕΈΝ–≥ωάϊ»σ±μ¥ο ΫΘ§Ζ÷±πΧ÷¬έάϊ»σΒΡΉν÷ΒΘ§Ήν÷’»ΓΖ÷ΕΈΚ· ΐ÷–Ϋœ¥σΒΡάϊ»σ÷Β.
ΫβΈωΘΚ
(1)”…ΥυΗχ ΐΨίΩ…ΒΟΘΚ ![]() Θ§
Θ§ ![]() Θ§
Θ§
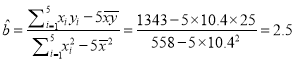 Θ§
Θ§ ![]() Θ§
Θ§
‘ρ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΈΣ
ΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΈΣ![]() .
.
(2)”…(1)÷–«σ≥ωΒΡœΏ–‘ΜΊΙιΖΫ≥Χ÷ΣΘ§Β±![]() ±Θ§
±Θ§ ![]() Θ§Φ¥‘ΛΦΤ–η“Σ‘≠≤ΡΝœ
Θ§Φ¥‘ΛΦΤ–η“Σ‘≠≤ΡΝœ![]() ¥ϋΘ§
¥ϋΘ§
“ρΈΣ![]() Θ§Υυ“‘Β±
Θ§Υυ“‘Β±![]() ±Θ§
±Θ§
άϊ»σ![]() Θ§Β±
Θ§Β±![]() ±Θ§
±Θ§ ![]() ΘΜ
ΘΜ
Β±![]() ±Θ§άϊ»σ
±Θ§άϊ»σ![]() Θ§Β±
Θ§Β±![]() ±Θ§
±Θ§ ![]() .
.
Ήέ…œΥυ ωΘ§≤ΆΧϋ”ΠΗΟΙΚ¬ρ36¥ϋ‘≠≤ΡΝœΘ§≤≈Ρή Ιάϊ»σΜώΒΟΉν¥σΘ§Ήν¥σάϊ»σΈΣ11870‘Σ.


 ÷«Μέ–ΓΗ¥œΑœΒΝ–¥πΑΗ
÷«Μέ–ΓΗ¥œΑœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥΙΡάχ –ΟώΫΎ‘Φ”ΟΒγΘ§ Β––ΓΑΫΉΧί ΫΓ±ΒγΦέΘ§Ρ≥±Ώ‘Ε…Ϋ«χΟΩΜßΨ”Οώ‘¬”ΟΒγΝΩΜ°Ζ÷ΈΣ»ΐΒΒΘΚ‘¬”ΟΒγΝΩ≤Μ≥§Ιΐ150Ε»Θ§Α¥0.6‘Σ/Ε» ’Ζ―Θ§≥§Ιΐ150Ε»ΒΪ≤Μ≥§Ιΐ250Ε»ΒΡ≤ΩΖ÷ΟΩΕ»Φ”Φέ0.1‘ΣΘ§≥§Ιΐ250Ε»ΒΡ≤ΩΖ÷ΟΩΕ»‘ΌΦ”Φέ0.3‘Σ ’Ζ―.
Θ®1Θ©«σΗΟ±Ώ‘Ε…Ϋ«χΡ≥ΜßΨ”Οώ‘¬”ΟΒγΖ―”Ο![]() Θ®ΒΞΈΜΘΚ‘ΣΘ©ΙΊ”Ύ‘¬”ΟΒγΝΩ
Θ®ΒΞΈΜΘΚ‘ΣΘ©ΙΊ”Ύ‘¬”ΟΒγΝΩ![]() Θ®ΒΞΈΜΘΚΕ»Θ©ΒΡΚ· ΐΫβΈω ΫΘΜ
Θ®ΒΞΈΜΘΚΕ»Θ©ΒΡΚ· ΐΫβΈω ΫΘΜ
Θ®2Θ©“―÷ΣΗΟ±Ώ‘Ε…Ϋ«χΤΕάßΜßΒΡ‘¬”ΟΒγΝΩ![]() Θ®ΒΞΈΜΘΚΕ»Θ©”κΗΟΜß≥ΛΤΎΨ”ΉΓΒΡ»ΥΩΎ ΐ
Θ®ΒΞΈΜΘΚΕ»Θ©”κΗΟΜß≥ΛΤΎΨ”ΉΓΒΡ»ΥΩΎ ΐ![]() Θ®ΒΞΈΜΘΚ»ΥΘ©ΦδΫϋΥΤΒΊ¬ζΉψœΏ–‘œύΙΊΙΊœΒΘΚ
Θ®ΒΞΈΜΘΚ»ΥΘ©ΦδΫϋΥΤΒΊ¬ζΉψœΏ–‘œύΙΊΙΊœΒΘΚ![]() Θ®
Θ®![]() ΒΡ÷ΒΨΪ»ΖΒΫ’ϊ ΐΘ©Θ§Τδ ΐΨί»γ±μΘΚ
ΒΡ÷ΒΨΪ»ΖΒΫ’ϊ ΐΘ©Θ§Τδ ΐΨί»γ±μΘΚ
| 14 | 15 | 17 | 18 |
| 161 | 168 | 191 | 200 |
œ÷’ΰΗ°ΈΣΦθ«αΤΕάßΦ“ΆΞΒΡΨ≠ΦΟΗΚΒΘΘ§ΦΤΜ°Ε‘ΗΟ±Ώ‘Ε…Ϋ«χΒΡΤΕάßΦ“ΆΞΫχ––“ΜΕ®ΒΡΨ≠ΦΟ≤Ι≥ΞΘ§Ηχ≥ωΝΫ÷÷≤Ι≥ΞΖΫΑΗΙ©―Γ‘ώΘΚ“Μ «ΗυΨίΗΟΦ“ΆΞ»Υ ΐΘ§ΟΩ»ΥΟΩΜß‘¬≤Ι≥Ξ6‘ΣΘΜΕΰ «ΗυΨί”ΟΒγΝΩΟΩ»ΥΟΩ‘¬≤Ι≥Ξ![]() Θ®
Θ®![]() ΈΣ”ΟΒγΝΩΘ©‘ΣΘ§«κΗυΨίΦ“ΆΞ»Υ ΐ
ΈΣ”ΟΒγΝΩΘ©‘ΣΘ§«κΗυΨίΦ“ΆΞ»Υ ΐ![]() Ζ÷ΈωΘ§“ΜΗωΤΕάßΦ“ΆΞ―Γ‘ώΡΡ÷÷≤Ι≥ΞΖΫ ΫΩ…“‘ΜώΒΟΗϋΕύΒΡ≤Ι≥ΞΘΩ
Ζ÷ΈωΘ§“ΜΗωΤΕάßΦ“ΆΞ―Γ‘ώΡΡ÷÷≤Ι≥ΞΖΫ ΫΩ…“‘ΜώΒΟΗϋΕύΒΡ≤Ι≥ΞΘΩ
ΗΫΘΚΜΊΙι÷±œΏ![]() ÷––±¬ ΚΆΫΊΨύΒΡΉν–ΓΕΰ≥ΥΖ®ΙάΦΤΙΪ ΫΖ÷±πΈΣΘΚ
÷––±¬ ΚΆΫΊΨύΒΡΉν–ΓΕΰ≥ΥΖ®ΙάΦΤΙΪ ΫΖ÷±πΈΣΘΚ
 Θ§
Θ§![]() .
.
≤ΈΩΦ ΐΨίΘΚ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§ΫΪ¥”ΒψM≥ωΖΔ―ΊΉίΓΔΚαΖΫœρΒΫ¥οΒψNΒΡ»Έ“Μ¬ΖΨΕ≥ΤΈΣMΒΫNΒΡ“ΜΧθΓΑL¬ΖΨΕΓ±Θ°»γΆΦΥυ ΨΒΡ¬ΖΨΕMM1M2M3N”κ¬ΖΨΕMN1NΕΦ «MΒΫNΒΡΓΑL¬ΖΨΕΓ±Θ°Ρ≥ΒΊ”–»ΐΗω–¬Ϋ®Ψ”Οώ«χΘ§Ζ÷±πΈΜ”ΎΤΫΟφxOyΡΎ»ΐΒψAΘ®3Θ§20Θ©Θ§BΘ®©¹10Θ§0Θ©Θ§CΘ®14Θ§0Θ©¥ΠΘ°œ÷ΦΤΜ°‘Ύx÷α…œΖΫ«χ”ρΘ®ΑϋΚ§x÷αΘ©ΡΎΒΡΡ≥“ΜΒψP¥Π–όΫ®“ΜΗωΈΡΜ·÷––ΡΘ°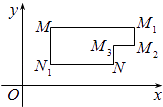
Θ®1Θ©–¥≥ωΒψPΒΫΨ”Οώ«χAΒΡΓΑL¬ΖΨΕΓ±≥ΛΕ»Ήν–Γ÷ΒΒΡ±μ¥ο ΫΘ®≤Μ“Σ«σ÷ΛΟςΘ©ΘΜ
Θ®2Θ©»τ“‘‘≠ΒψOΈΣ‘≤–ΡΘ§ΑκΨΕΈΣ1ΒΡ‘≤ΒΡΡΎ≤Ω «±ΘΜΛ«χΘ§ΓΑL¬ΖΨΕΓ±≤ΜΡήΫχ»κ±ΘΜΛ«χΘ§«κ»ΖΕ®ΒψPΒΡΈΜ÷ΟΘ§ ΙΤδΒΫ»ΐΗωΨ”Οώ«χΒΡΓΑL¬ΖΨΕΓ±≥ΛΕ»÷°ΚΆΉν–ΓΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ―Γ–ό4-5ΘΚ≤ΜΒ» Ϋ―ΓΫ≤
“―÷ΣΚ· ΐ![]() .
.
Θ®1Θ©«σ≤ΜΒ» Ϋ![]() ΒΡΫβΦ·ΘΜ
ΒΡΫβΦ·ΘΜ
Θ®2Θ©»τ![]() Ε‘
Ε‘![]() Κψ≥…ΝΔΘ§«σ
Κψ≥…ΝΔΘ§«σ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§≈ΉΈοœΏ
÷–Θ§≈ΉΈοœΏ![]() ΒΡΫΙΒψΈΣ
ΒΡΫΙΒψΈΣ![]() Θ§Βψ
Θ§Βψ![]() «≈ΉΈοœΏ
«≈ΉΈοœΏ![]() …œ“ΜΒψΘ§«“
…œ“ΜΒψΘ§«“![]() Θ°
Θ°
Θ®1Θ©«σ![]() ΒΡ÷ΒΘΜ
ΒΡ÷ΒΘΜ
Θ®2Θ©»τ![]() ΈΣ≈ΉΈοœΏ
ΈΣ≈ΉΈοœΏ![]() …œ“λ”Ύ
…œ“λ”Ύ![]() ΒΡΝΫΒψΘ§«“
ΒΡΝΫΒψΘ§«“![]() Θ°Φ«Βψ
Θ°Φ«Βψ![]() ΒΫ÷±œΏ
ΒΫ÷±œΏ![]() ΒΡΨύάκΖ÷±πΈΣ
ΒΡΨύάκΖ÷±πΈΣ![]() Θ§«σ
Θ§«σ![]() ΒΡ÷ΒΘ°
ΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΦΌ…ηΟΩΧλ¥”ΦΉΒΊ»Ξ““ΒΊΒΡ¬ΟΩΆ»Υ ΐX «Ζΰ¥”’ΐΧ§Ζ÷≤ΦNΘ®800Θ§502Θ©ΒΡΥφΜζ±δΝΩΘ°Φ«“ΜΧλ÷–¥”ΦΉΒΊ»Ξ““ΒΊΒΡ¬ΟΩΆ»Υ ΐ≤Μ≥§Ιΐ900ΒΡΗ≈¬ ΈΣp0 Θ°
Θ®1Θ©«σp0ΒΡ÷ΒΘΜ
Θ®≤ΈΩΦ ΐΨίΘΚ»τXΓΪNΘ®ΠΧΘ§Π“2Θ©Θ§”–PΘ®ΠΧ©¹Π“ΘΦXΓήΠΧ+Π“Θ©=0.6826Θ§PΘ®ΠΧ©¹2Π“ΘΦXΓήΠΧ+2Π“Θ©=0.9544Θ§PΘ®ΠΧ©¹3Π“ΘΦXΓήΠΧ+3Π“Θ©=0.9974Θ°Θ©
Θ®2Θ©Ρ≥ΩΆ‘ΥΙΪΥΨ”ΟAΘ§BΝΫ÷÷–ΆΚ≈ΒΡ≥ΒΝΨ≥–ΒΘΦΉΓΔ““ΝΫΒΊΦδΒΡ≥ΛΆΨΩΆ‘Υ“ΒΈώΘ§ΟΩ≥ΒΟΩΧλΆυΖΒ“Μ¥ΈΘ§AΘ§BΝΫ÷÷≥ΒΝΨΒΡ‘ΊΩΆΝΩΖ÷±πΈΣ36»ΥΚΆ60»ΥΘ§¥”ΦΉΒΊ»Ξ““ΒΊΒΡ”Σ‘Υ≥…±ΨΖ÷±πΈΣ1600‘Σ/ΝΨΚΆ2400‘Σ/ΝΨΘ°ΙΪΥΨΡβΉιΫ®“ΜΗω≤Μ≥§Ιΐ21ΝΨ≥ΒΒΡΩΆ‘Υ≥ΒΕ”Θ§≤Δ“Σ«σB–Ά≥Β≤ΜΕύ”ΎA–Ά≥Β7ΝΨΘ°»τΟΩΧλ“Σ“‘≤Μ–Γ”Ύp0ΒΡΗ≈¬ ‘ΥΆξ¥”ΦΉΒΊ»Ξ““ΒΊΒΡ¬ΟΩΆΘ§«“ ΙΙΪΥΨ¥”ΦΉΒΊ»Ξ““ΒΊΒΡ”Σ‘Υ≥…±ΨΉν–ΓΘ§Ρ«Ο¥”Π≈δ±ΗA–Ά≥ΒΓΔB–Ά≥ΒΗςΕύ…ΌΝΨΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() .
.
Θ®1Θ©Β±![]() ±Θ§«σ
±Θ§«σ![]() ΒΡΦΪ÷ΒΘΜ
ΒΡΦΪ÷ΒΘΜ
Θ®2Θ©Β±![]() ±Θ§Χ÷¬έ
±Θ§Χ÷¬έ![]() ΒΡΒΞΒς–‘ΘΜ
ΒΡΒΞΒς–‘ΘΜ
Θ®3Θ©»τΕ‘»Έ“βΒΡ![]() Θ§
Θ§![]() Θ§Κψ”–
Θ§Κψ”–![]() ≥…ΝΔΘ§«σ Β ΐ
≥…ΝΔΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈß.
ΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηΚ· ΐ![]() Θ§Τδ÷–
Θ§Τδ÷–![]() .
.
Θ®ΔώΘ©Β±![]() ±Θ§«σΚ· ΐ
±Θ§«σΚ· ΐ![]() ΒΡΦΪ÷ΒΘΜ
ΒΡΦΪ÷ΒΘΜ
Θ®ΔρΘ©Β±![]() ±Θ§÷ΛΟςΘΚΚ· ΐ
±Θ§÷ΛΟςΘΚΚ· ΐ![]() ≤ΜΩ…Ρή¥φ‘ΎΝΫΗωΝψΒψ.
≤ΜΩ…Ρή¥φ‘ΎΝΫΗωΝψΒψ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ§
Θ§![]() .
.
Θ®1Θ©Χ÷¬έ![]() ΒΡΒΞΒς–‘ΘΜ
ΒΡΒΞΒς–‘ΘΜ
Θ®2Θ©»τ![]() ”–ΝΫΗωΦΪ÷ΒΒψ
”–ΝΫΗωΦΪ÷ΒΒψ![]() Θ§
Θ§![]() Θ§«“
Θ§«“![]() Θ§÷ΛΟςΘΚ
Θ§÷ΛΟςΘΚ![]() .
.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com