
| n |
| n+1 |
| 1 |
| n |
| A.①③ | B.②③ | C.①④ | D.②④ |
| a |
| 2 |
| a |
| 2 |
| n |
| n+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| n |
| n+1 |
| 1 |
| n |
| 1 |
| a |
| 1 |
| n |
| 1 |
| n |


科目:高中数学 来源: 题型:
| n |
| n+1 |
| 1 |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
![]() 已知{an}是等差数列,d为公差且不为0,a1和d均为实数,它的前n项和记作Sn,设集合A={(an,
已知{an}是等差数列,d为公差且不为0,a1和d均为实数,它的前n项和记作Sn,设集合A={(an,![]() )|n∈N*},B={(x,y)|
)|n∈N*},B={(x,y)|![]() x2-y2=1,x,y∈R}.
x2-y2=1,x,y∈R}.
试问下列结论是否正确,如果正确,请给予证明;如果不正确,请举例说明![]()
(1)若以集合A中的元素作为点的坐标,则这些点都在同一条直线上;
(2)A∩B至多有一个元素;
(3)当a1≠0时,一定有A∩B≠![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 |n∈Z,n≥0};
|n∈Z,n≥0};  |n∈Z,n≠0}.
|n∈Z,n≠0}.查看答案和解析>>
科目:高中数学 来源:2010-2011学年北京市西城区(北区)高二(下)期末数学试卷(文科)(解析版) 题型:选择题
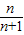 |n∈Z,n≥0};
|n∈Z,n≥0}; 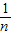 |n∈Z,n≠0}.
|n∈Z,n≠0}.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com