
【题目】已知函数![]() ,
, ![]()
![]() 且
且![]() .
.
(1)当![]() 时,设集合
时,设集合![]() ,求集合
,求集合![]() ;
;
(2)在(1)的条件下,若![]() ,且满足
,且满足![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)若对任意的![]() ,存在
,存在![]() ,使不等式
,使不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】已知在△ABC中,角A,B,C的对边分别是a,b,c,且bsinA+acosB=0.
(1)求角B的大小;
(2)若b=2,求△ABC面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的一个上界.已知函数
的一个上界.已知函数![]() ,
, ![]() .
.
(1)若函数![]() 为奇函数,求实数
为奇函数,求实数![]() 的值;
的值;
(2)在(1)的条件下,求函数![]() 在区间
在区间![]() 上的所有上界构成的集合;
上的所有上界构成的集合;
(3)若函数![]() 在
在![]() 上是以3为上界的有界函数,求实数
上是以3为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知首项为 ![]() 的等比数列
的等比数列 ![]() 是递减数列,且
是递减数列,且 ![]() ,
, ![]() ,
, ![]() 成等差数列;数列
成等差数列;数列 ![]() 的前
的前 ![]() 项和为
项和为 ![]() ,且
,且 ![]() ,
, ![]()
(Ⅰ)求数列 ![]() ,
, ![]() 的通项公式;
的通项公式;
(Ⅱ)已知 ![]() ,求数列
,求数列 ![]() 的前
的前 ![]() 项和
项和 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
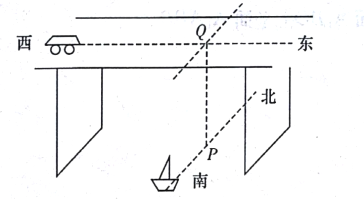
【题目】一只小船以![]() 的速度由南向北匀速驶过湖面,在离湖面高20米的桥上,一辆汽车由西向东以
的速度由南向北匀速驶过湖面,在离湖面高20米的桥上,一辆汽车由西向东以![]() 的速度前进(如图),现在小船在水平面上的
的速度前进(如图),现在小船在水平面上的![]() 点以南的40米处,汽车在桥上
点以南的40米处,汽车在桥上![]() 点以西的30米处(其中
点以西的30米处(其中![]() 水平面),请画出合适的空间图形并求小船与汽车间的最短距离.(不考虑汽车与小船本身的大小).
水平面),请画出合适的空间图形并求小船与汽车间的最短距离.(不考虑汽车与小船本身的大小).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 的定义域为R
的定义域为R
(1)当a=2时,求函数f(x)的值域
(2)若函数f(x)是奇函数,①求a的值;②解不等式f(3﹣m)+f(3﹣m2)>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在(1+x+x2)n= ![]() x
x ![]() x2+…
x2+… ![]() xr+…
xr+… ![]() x2n﹣1
x2n﹣1 ![]() x2n的展开式中,把D
x2n的展开式中,把D ![]() ,D
,D ![]() ,D
,D ![]() …,D
…,D ![]() …,D
…,D ![]() 叫做三项式系数
叫做三项式系数
(1)求D ![]() 的值
的值
(2)根据二项式定理,将等式(1+x)2n=(1+x)n(x+1)n的两边分别展开可得,左右两边xn的系数相等,即C ![]() =(C
=(C ![]() )2+(C
)2+(C ![]() )2+(C
)2+(C ![]() )2+…+(C
)2+…+(C ![]() )2 , 利用上述思想方法,请计算D
)2 , 利用上述思想方法,请计算D ![]() C
C ![]() ﹣D
﹣D ![]() C
C ![]() +D
+D ![]() C
C ![]() ﹣…+(﹣1)rD
﹣…+(﹣1)rD ![]() C
C ![]() +..
+.. ![]() C
C ![]() C
C ![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,动点P从单位正方形ABCD顶点A开始,顺次经B、C、D绕边界一周,当![]() 表示点P的行程,
表示点P的行程, ![]() 表示PA之长时,求y关于x的解析式,并求
表示PA之长时,求y关于x的解析式,并求![]() 的值.
的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:关于x的方程x2﹣ax+4=0有实根;命题q:关于x的函数y=2x2+ax+4在[3,+∞)上是增函数,若p∧q是真命题,则实数a的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com