
【题目】某数学小组从医院和气象局获得2018年1月至6月份每月20的昼夜温差![]() ,(
,(![]() )和患感冒人数(
)和患感冒人数(![]() /人)的数据,画出如图的折线图.
/人)的数据,画出如图的折线图.
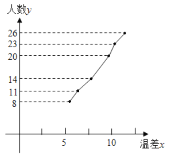
(1)建立![]() 关于
关于![]() 的回归方程(精确到0.01),预测2019年1月至6月份昼夜温差为
的回归方程(精确到0.01),预测2019年1月至6月份昼夜温差为![]() 时患感冒的人数(精确到整数);
时患感冒的人数(精确到整数);
(2)求![]() 与
与![]() 的相关系数,并说明
的相关系数,并说明![]() 与
与![]() 的相关性的强弱(若
的相关性的强弱(若![]() ,则认为
,则认为![]() 与
与![]() 具有较强的相关性),
具有较强的相关性),
参考数据:![]() ,
,![]() ,
,![]() ,
,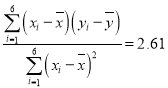 ,
,![]()
相关系数: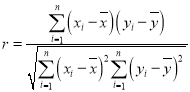 ,回归直线方程是
,回归直线方程是![]() ,
,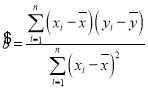 ,
,![]()
科目:高中数学 来源: 题型:
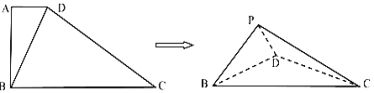
【题目】如图,在直角梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() ,将直角梯形
,将直角梯形![]() 沿对角线
沿对角线![]() 折起,使点
折起,使点![]() 到
到![]() 点位置,则四面体
点位置,则四面体![]() 的体积的最大值为________,此时,其外接球的表面积为________.
的体积的最大值为________,此时,其外接球的表面积为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若存在![]() ,使得
,使得![]() 对任意
对任意![]() 恒成立,则函数
恒成立,则函数![]() 在
在![]() 上有下界,其中
上有下界,其中![]() 为函数
为函数![]() 的一个下界;若存在
的一个下界;若存在![]() ,使得
,使得![]() 对任意
对任意![]() 恒成立,则函数
恒成立,则函数![]() 在
在![]() 上有上界,其中
上有上界,其中![]() 为函数
为函数![]() 的一个上界.如果一个函数既有上界又有下界,那么称该函数有界.
的一个上界.如果一个函数既有上界又有下界,那么称该函数有界.
下述四个结论:①1不是函数![]() 的一个下界;②函数
的一个下界;②函数![]() 有下界,无上界;③函数
有下界,无上界;③函数![]() 有上界,无下界;④函数
有上界,无下界;④函数![]() 有界.
有界.
其中所有正确结论的编号是( )
A.①②B.②④C.③④D.②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆上,且
在椭圆上,且![]() 轴,
轴,![]() 的周长为6.
的周长为6.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,设
两点,设![]() 为坐标原点,是否存在常数
为坐标原点,是否存在常数![]() ,使得
,使得![]() 恒成立?请说明理由.
恒成立?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,
,![]() 是椭圆
是椭圆![]() 的三个顶点,椭圆的离心率
的三个顶点,椭圆的离心率![]() ,点
,点![]() 到直线
到直线![]() 的距离是
的距离是![]() .设
.设![]() 是椭圆上位于
是椭圆上位于![]() 轴左边上的任意一点,直线
轴左边上的任意一点,直线![]() ,
,![]() 分别交直线
分别交直线![]() 于
于![]() ,
,![]() 两点,以
两点,以![]() 为直径的圆记为
为直径的圆记为![]() .
.
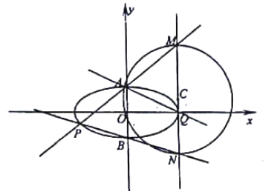
(1)求椭圆的方程;
(2)求证:圆![]() 始终与圆
始终与圆![]() :
:![]() 相切,并求出所有圆
相切,并求出所有圆![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥M-ABCD中,MB⊥平面ABCD,四边形ABCD是矩形,AB=MB,E、F分别为MA、MC的中点.
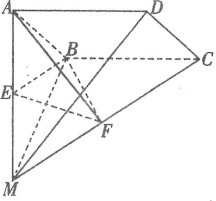
(1)求证:平面BEF⊥平面MAD;
(2)若![]() ,求三棱锥E-ABF的体积.
,求三棱锥E-ABF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=![]() .则下列结论中正确的个数为
.则下列结论中正确的个数为
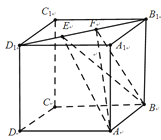
①AC⊥BE;
②EF∥平面ABCD;
③三棱锥A﹣BEF的体积为定值;
④![]() 的面积与
的面积与![]() 的面积相等,
的面积相等,
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,在
,在![]() 轴上,是否存在点
轴上,是否存在点![]() ,使得无论非零实数
,使得无论非零实数![]() 怎样变化,总有
怎样变化,总有![]() 为直角?若存在,求出点
为直角?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com