
![]()
B.甲:ab<0,乙:|a+b|<|a-b|
![]()

| 分析 如果不等式是关于自然数命题的形式,又无好的切入点时,不妨试用数学归纳法来证明.
证明:(1)当n=1时,左边=(a+b)-(a+b)=0,右边=22-22=0,所以左=右,因此原不等式成立. (2)假设n=k时,不等式成立,即(a+b)k-(ak+bk)≥22k-2k+1.则n=k+1
于是有ab=a+b≥4.因此 (a+b)k+1-(ak+1+bk+1) =(a+b)(a+b)k-(a+b)(ak+bk)+(a+b)(ak+bk)-(ak+1+bk+1) =(a+b)[(a+b)k-(ak+bk)]+(ak+1+bk+1)+abk+bak-(ak+1+bk+1)
所以n=k+1时,原不等式成立. <综合(1),(2),对于任意的自然数n,原不等式成立.
|


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源:高中新教材辅导 数学高中一年级 题型:013
下列四组条件中,甲是乙的充分不必要条件的是
[ ]
A.甲:a>b,乙:![]()
B.甲:ab<0,乙:|a+b|<|a-b|
C.甲:a=b,乙:a+b=![]()
D.甲: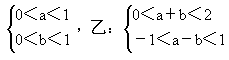
查看答案和解析>>
科目:高中数学 来源:成功之路·突破重点线·数学(学生用书) 题型:013
下列四组条件中,甲是乙的充分不必要条件的是
[ ]
A.甲:a>b,乙:![]() <
<![]() ,
,
B.甲:ab<0,乙:|a+b|<|a-b|
C.甲:a=b,乙:a+b=2![]()
D.甲:![]() 乙:
乙:![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
下列四组条件中,甲是乙的充分不必要条件的是( )
A. 甲 a>b,乙 ![]() <
<![]() B 甲 ab<0,乙 a+b<a-b
B 甲 ab<0,乙 a+b<a-b
C 甲 a=b ,![]() 乙 a+b=2
乙 a+b=2![]() D 甲
D 甲 ![]() ,乙
,乙 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com