练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （本小题10分）△ABC中，D在边BC上，且BD＝2，DC＝1，∠B＝60o，∠ADC＝150o，求AC的长及△ABC的面积．

     

    【答案】

    AC＝．S△ABC＝

    【解析】

    试题分析：解：在△ABC中，∠BAD＝150o－60o＝90o，∴AD＝2sin60o＝．

    在△ACD中，AD2＝()2＋12－2××1×cos150o＝7，∴AC＝．

    ∴AB＝2cos60o＝1．S△ABC＝×1×3×sin60o＝．

    考点：余弦定理

    点评：解决该试题关键是利用已知中的边和角，确定运用余弦定理来解三角形，属于基础题。

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    必做题，本小题10分．解答时应写出文字说明、证明过程或演算步骤．
    已知抛物线y2=4x的焦点为F，直线l过点M（4，0）．
    （1）若点F到直线l的距离为
    		3
    ，求直线l的斜率；
    （2）设A，B为抛物线上两点，且AB不与x轴垂直，若线段AB的垂直平分线恰过点M，求证：线段AB中点的横坐标为定值．（6分）

    查看答案和解析>>

    科目：高中数学 来源：2013届甘肃省天水市一中高三第三次考试文科数学试卷（带解析） 题型：解答题

    （本小题10分）已知函数当时，求不等式的解集；若的解集包含，求a的取值范围。

    查看答案和解析>>

    科目：高中数学 来源：2012年苏教版高中数学选修2-2 3.1数系的扩充练习卷（解析版） 题型：解答题

    (本小题10分)已知z= (a>0,a∈R),复数ω=z(z+i)的虚部减去它的实部所得的差是，求复数ω.

     

    查看答案和解析>>

    科目：高中数学 来源：2011-2012年浙江省高二第一学期期中考试理科数学 题型：解答题

    （（本小题10分） 已知椭圆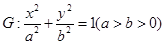的两个焦点为、，点在椭圆G上，且，且，斜率为1的直线与椭圆G交与A、B两点，以AB为底边作等腰三角形，顶点为P（-3,2）.

        （1）求椭圆G的方程；

        （2）求的面积.

     

     

    查看答案和解析>>

    科目：高中数学 来源：2010年福建省高二上学期期中考试数学卷 题型：解答题

    （本小题10分）

    已知△ABC的内角A、B、C所对的边分别为a，b，c，且a=2， cosB=．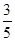

    (1)若b=4，求sinA的值；

     (2) 若△ABC的面积S△ABC=4，求b，c的值．

     

    查看答案和解析>>

    同步练习册答案