
分析 f(x)=x2+a|x-1|=$\left\{\begin{array}{l}{{x}^{2}+ax-a,x≥1}\\{{x}^{2}-ax+a,x<1}\end{array}\right.$,结合题意可得函数y=x2+ax-a在[1,+∞)单调递增,y=x2-ax+a在[0,1)单调递增,故有 $\left\{\begin{array}{l}{-\frac{a}{2}≤1}\\{\frac{a}{2}≤0}\\{1-a+a≤1+a-a}\end{array}\right.$,由此求得实数a的取值范围.
解答 解:∵f(x)=x2+a|x-1|=$\left\{\begin{array}{l}{{x}^{2}+ax-a,x≥1}\\{{x}^{2}-ax+a,x<1}\end{array}\right.$,
∴要使f(x)在[0,+∞)上单调递增,需函数y=x2+ax-a在[1,+∞)单调递增,
且y=x2-ax+a在[0,1)单调递增,故有 $\left\{\begin{array}{l}{-\frac{a}{2}≤1}\\{\frac{a}{2}≤0}\\{1-a+a≤1+a-a}\end{array}\right.$,
求得-2≤a≤0,∴实数a的取值范围是[-2,0],
故答案为:[-2,0].
点评 本题主要考查含绝对值函数的单调性,二次函数的单调性及单调区间,属于中档题.


 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
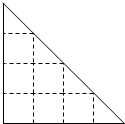 网上有一项虚似的游戏,在如图所示的等腰直角三角形上有15个格点(横、纵相邻格点间的距离为1个单位),三角形边界上的每个格点记1分,三角形内部的每个格点记2分,若点击鼠标左键,屏幕上会随机等可能地显示点中的某一格点,点中某格点后,将与其距离为1个单位的格点的分数和作为其得分.
网上有一项虚似的游戏,在如图所示的等腰直角三角形上有15个格点(横、纵相邻格点间的距离为1个单位),三角形边界上的每个格点记1分,三角形内部的每个格点记2分,若点击鼠标左键,屏幕上会随机等可能地显示点中的某一格点,点中某格点后,将与其距离为1个单位的格点的分数和作为其得分.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | [0,1) | C. | [-1,1] | D. | [-1,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 当m∈$(\frac{2}{3},+∞)$时,函数h(x)无零点 | |
| B. | 当m∈$(-∞,\frac{2}{3})$时,函数h(x)恰有一个零点 | |
| C. | 当m∈$[0,\frac{2}{3}]$时,函数h(x)恰有两个零点 | |
| D. | 当m∈$(-\frac{2}{3},\frac{2}{3})$时,函数h(x)恰有三个零点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5π}{3}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{2}$ | D. | $\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com