
 ,最后在Rt△GCD中,计算出∠GCD的余弦值为
,最后在Rt△GCD中,计算出∠GCD的余弦值为 ,可得∠GCD=45°,从而AC与平面β所成的角等于45°.
,可得∠GCD=45°,从而AC与平面β所成的角等于45°.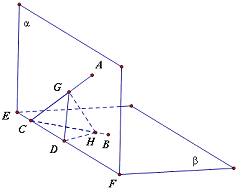 在平面α内过G点作GD⊥EF于D,在平面β内过点D作DH⊥BC于H,连接GH
在平面α内过G点作GD⊥EF于D,在平面β内过点D作DH⊥BC于H,连接GH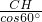 =2,
=2,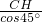 =
=
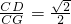 ,可得∠GCD=45°
,可得∠GCD=45°

科目:高中数学 来源: 题型:
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 二面角α-EF-β的大小为120°,A是它内部的一点AB⊥α,AC⊥β,B,C分别为垂足.
二面角α-EF-β的大小为120°,A是它内部的一点AB⊥α,AC⊥β,B,C分别为垂足.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,边长为2的正方形ABCD中,点E、F分别是边AB、BC上的点,将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A′.
如图,边长为2的正方形ABCD中,点E、F分别是边AB、BC上的点,将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A′.查看答案和解析>>
科目:高中数学 来源:2013届辽宁省高二下学期期中考试理科数学试卷(解析版) 题型:填空题
二面角α—EF—β是直二面角,C∈EF,AC 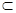 α,BC
α,BC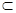 β,∠ACF=30°
β,∠ACF=30°
∠ACB=60°,则∠BCF等于 。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com