|
|
|
“cosα>0”是“x2+y2cosα=1表示焦点在y轴上的椭圆”的( )条件
|
| [ ] |
A. |
充分而非必要
|
B. |
充要
|
C. |
必要而非充分
|
D. |
既非充分又非必要
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:人民教育出版社 代数
题型:
|
|
|
如果复数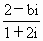 (其中i为虚数单位,b为实数)的实部和虚部互为相反数,那么b等 (其中i为虚数单位,b为实数)的实部和虚部互为相反数,那么b等
|
| [ ] |
A. |
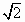
|
B. |
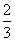
|
C. |
-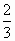
|
D. |
2
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社(实验修订本) 高中数学
题型:
|
|
|
已知函数f(x)=x(x-a)2在x=2处取得极小值,则实数a的值为:________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:人民教育出版社(实验修订本) 高中数学
题型:
|
|
|
已知平面向量a=(1,2),b=(-2,m),且a∥b,则m的值为
|
| [ ] |
A. |
1
|
B. |
-1
|
C. |
4
|
D. |
-4
|
|
|
查看答案和解析>>
科目:高中数学
来源:人教版(大纲版) 高中数学
题型:
|
|
|
“cosα>0”是“x2+y2cosα=1表示焦点在y轴上的椭圆”的( )条件
|
| [ ] |
A. |
充分而非必要
|
B. |
充要
|
C. |
必要而非充分
|
D. |
既非充分又非必要
|
|
|
查看答案和解析>>
科目:高中数学
来源:人教B版(新课标) 必修1
题型:
|
|
|
已知f(2)=- (2)=-2,g(2)= (2)=-2,g(2)= (2)=1,函数F(x)=f(x)[g(x)-2],则 (2)=1,函数F(x)=f(x)[g(x)-2],则 (2)= (2)=
|
| [ ] |
A. |
-5
|
B. |
5
|
C. |
-3
|
D. |
3
|
|
|
查看答案和解析>>
科目:高中数学
来源:人教B版(新课标) 必修3
题型:
|
|
|
某高中采用系统抽样的方法从该校高一年级1600名学生中抽取50名学生作视力健康检查.现将1600名学生从1到1600进行编号.已知从65~96这32个数中取的数是78,则在第1小组1~32中抽到的数是________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:人教B版(新课标) 选修1-2
题型:
|
|
|
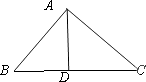
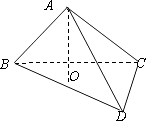
类比平面几何中的射影定理:若直角三角形ABC中(如图),AB、AC互相垂直,AD是BC边的高,则AB2=BD·BC;AC2=CD·BC.若在三棱锥A-BCD中(如图),三个侧面ABC、ACD、ADB两两互相垂直,O是点A在平面BCD上的投影,则三棱锥的侧面面积与它在底面上的投影面积和底面积的之间满足的关系为________(只需填一个)
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
x,y满足约束条件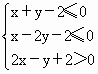 ,若z=y-ax取得最大值的最优解不唯一,则实数a的值为 ,若z=y-ax取得最大值的最优解不唯一,则实数a的值为
|
| [ ] |
A. |
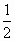 或-1 或-1
|
B. |
2或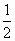
|
C. |
2或1
|
D. |
2或-1
|
|
|
查看答案和解析>>

 阅读快车系列答案
阅读快车系列答案