已知全集U=R,集合A={x||x|<3},B={x|x2-x-6>0},M={x|x2+bx+c≥0},
(1)求A∩B;
(2)若CUM=A∩B,求b,c的值.
解:(1)A={ x||x|<3}={x|-3<x<3},B={x|x
2-x-6>0}={x|x<-2,或x>3},
∴A∩B={x|-3<x<-2}.
(2)由C
UM=A∩B={x|-3<x<-2} 得M={x|x≥-2,或x≤-3}.
所以方程x
2+bx+c=0 有两根,即 x=-2,或x=-3.
由韦达定理得:

,即:
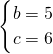
.
分析:(1)解绝对值不等式求得A,解一元二次不等式求得B,再利用两个集合的交集的定义求得A∩B.
(2)由题意可得得方程x
2+bx+c=0 有两根,即 x=-2,或x=-3,利用一元二次方程根与系数的关系求得b,c的值.
点评:本题主要考查集合关系中参数的取值范围问题,补集的定义、两个集合的交集的定义和求法,属于基础题.

 ,即:
,即: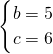 .
.

 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案