
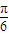 ),x∈R.
),x∈R.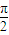 ]上的值域;
]上的值域; ,且a=
,且a=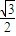 b,求角B的值.
b,求角B的值.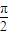 ]上的值域;
]上的值域;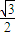 ,得出sin(A+
,得出sin(A+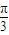 )的值,利用特殊角的三角函数值求出A的度数,确定出sinA的值,再利用正弦定理利用关系式,将已知的等式a=
)的值,利用特殊角的三角函数值求出A的度数,确定出sinA的值,再利用正弦定理利用关系式,将已知的等式a=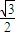 b及sinA的值代入,求出sinB的值,由B为三角形的内角,利用特殊角的三角函数值即可求出B的度数.
b及sinA的值代入,求出sinB的值,由B为三角形的内角,利用特殊角的三角函数值即可求出B的度数.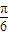 )
)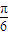 -sinxsin
-sinxsin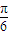
 sinx+
sinx+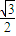 cosx
cosx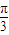 ),
),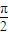 ],∴x+
],∴x+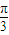 ∈[
∈[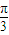 ,
,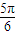 ],
], ,1];
,1];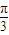 )=
)=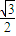 ,
,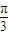 <A+
<A+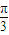 <
<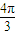 ,
,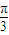 =
=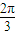 ,即A=
,即A=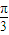 ,
,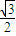 b,且
b,且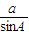 =
=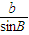 ,
,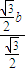 =
=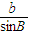 ,即sinB=1,
,即sinB=1,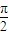 .
.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:
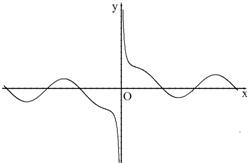 如图是函数Q(x)的图象的一部分,设函数f(x)=sinx,g ( x )=
如图是函数Q(x)的图象的一部分,设函数f(x)=sinx,g ( x )=| 1 |
| x |
A、
| ||
| B、f(x)g(x) | ||
| C、f(x)-g(x) | ||
| D、f(x)+g(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| bc |
| b2+c2-a2 |
| 1 |
| 2 |
| π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| sinx+cosx-|sinx-cosx| |
| 2 |
| ||
| 2 |
| 5π |
| 3 |
| 17π |
| 6 |
| 5π |
| 3 |
| 17π |
| 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com