
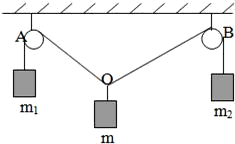
 如图所示,对于同一高度(足够高)的两个定滑轮A、B,用一条足够长的绳子跨过它们,并在两端分别挂有质量为m1和m2的物体(m1≠m2),另在两滑轮中间的一段绳子的O点处悬挂质量为m的另一物体,已知m1:m2=OB:OA,且系统保持平衡(滑轮半径、绳子质量均忽略不计).求证:
如图所示,对于同一高度(足够高)的两个定滑轮A、B,用一条足够长的绳子跨过它们,并在两端分别挂有质量为m1和m2的物体(m1≠m2),另在两滑轮中间的一段绳子的O点处悬挂质量为m的另一物体,已知m1:m2=OB:OA,且系统保持平衡(滑轮半径、绳子质量均忽略不计).求证: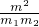 >2.
>2.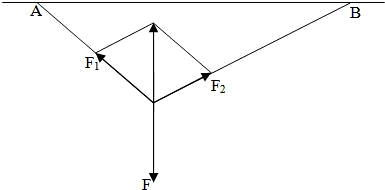 解:(1)设两绳子AO、BO对物体m的拉力分别为F1、F2,物体m向下的重力为F,由系统平衡条件知F1+F2+F=0.
解:(1)设两绳子AO、BO对物体m的拉力分别为F1、F2,物体m向下的重力为F,由系统平衡条件知F1+F2+F=0.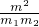 >2.
>2.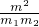 >2.原式得证.
>2.原式得证.

科目:高中数学 来源: 题型:
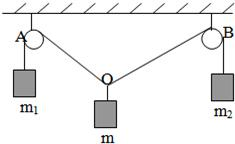 如图所示,对于同一高度(足够高)的两个定滑轮A、B,用一条足够长的绳子跨过它们,并在两端分别挂有质量为m1和m2的物体(m1≠m2),另在两滑轮中间的一段绳子的O点处悬挂质量为m的另一物体,已知m1:m2=OB:OA,且系统保持平衡(滑轮半径、绳子质量均忽略不计).求证:
如图所示,对于同一高度(足够高)的两个定滑轮A、B,用一条足够长的绳子跨过它们,并在两端分别挂有质量为m1和m2的物体(m1≠m2),另在两滑轮中间的一段绳子的O点处悬挂质量为m的另一物体,已知m1:m2=OB:OA,且系统保持平衡(滑轮半径、绳子质量均忽略不计).求证:| m2 | m1m2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
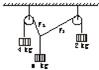 如图所示,对于同一高度(足够高)的两个定滑轮,用一条(足够长)绳子跨过它们,并在两端分别挂有4 kg和2 kg的物体,另在两个滑轮中间的一段绳子悬挂另一物体,为使系统保持平衡状态,此物体的质量应是多少?(忽略滑轮半径、绳子的重量)
如图所示,对于同一高度(足够高)的两个定滑轮,用一条(足够长)绳子跨过它们,并在两端分别挂有4 kg和2 kg的物体,另在两个滑轮中间的一段绳子悬挂另一物体,为使系统保持平衡状态,此物体的质量应是多少?(忽略滑轮半径、绳子的重量)查看答案和解析>>
科目:高中数学 来源: 题型:
假设两个分类变量X与Y,它们的取值分别为{x1,x2},{y1,y2},其2×2列联表如图所示:对于以下数据,对同一样本能说明X与Y有关的可能性最大的一组为( )
|
查看答案和解析>>
科目:高中数学 来源:2006年高考第一轮复习数学:5.5 向量的应用(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com