
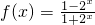 .
.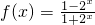 的定义域为R,关于原点对称,且有f(-x)=
的定义域为R,关于原点对称,且有f(-x)= =
= =-
=- =-f(x),故函数f(x)为奇函数.
=-f(x),故函数f(x)为奇函数.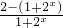 =
= -1,设x1<x2,再由f(x1)-f(x2)=(
-1,设x1<x2,再由f(x1)-f(x2)=(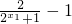 )-(
)-(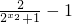 )=
)=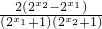 >0,
>0, ,
, ).
). -1,设x1<x2,化简f(x1)-f(x2)=
-1,设x1<x2,化简f(x1)-f(x2)=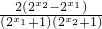 >0,可得函数f(x)在R上是减函数.
>0,可得函数f(x)在R上是减函数.

科目:高中数学 来源: 题型:
 (2012•江苏二模)如图,在C城周边已有两条公路l1,l2在点O处交汇,现规划在公路l1,l2上分别选择A,B两处为交汇点(异于点O)直接修建一条公路通过C城,已知OC=(
(2012•江苏二模)如图,在C城周边已有两条公路l1,l2在点O处交汇,现规划在公路l1,l2上分别选择A,B两处为交汇点(异于点O)直接修建一条公路通过C城,已知OC=(| 2 |
| 6 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省泰安市高三(上)期中数学试卷(理科)(解析版) 题型:解答题
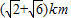 ,∠AOB=75°,∠AOC=45°,设OA=xkm,OB=ykm.
,∠AOB=75°,∠AOC=45°,设OA=xkm,OB=ykm.
查看答案和解析>>
科目:高中数学 来源:2012年江苏省苏北四市高考数学二模试卷(解析版) 题型:解答题
 ,∠AOB=75°,∠AOC=45°,设OA=xkm,OB=ykm.
,∠AOB=75°,∠AOC=45°,设OA=xkm,OB=ykm.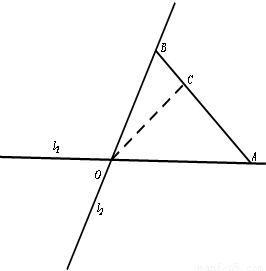
查看答案和解析>>
科目:高中数学 来源: 题型:
(Ⅰ)试确a,b的值;
(Ⅱ)讨论函数f(x)的单调区向;
(Ⅲ)若对任意x>0,不等式f(x)≥-2c2恒成立,求x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com