Question

正四棱锥的底面积为Q，侧面积为P，侧面与底面所成的二面角为α，则cosα=    ．

Answer 1

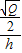
【答案】分析：我们作出满足条件的图形，过点S做垂直于底边AB的直线SE，并则设SE长为h由已知中正四棱锥的底面积为Q，侧面积为P，可将h用P，Q表示，代入cosα=，整理即可得到答案．
解答：解：如图，正四棱锥S-ABCD中
过点S做垂直于底边AB的直线SE
则设SE长为h，底面的边长为根号Q．
正四棱锥的一个侧面面积为P，
则h=
因为正四棱锥的侧面的等腰三角形的高都是h，
则cosα===
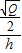
故答案为：
点评：本题考查的知识点是二面角的平面角及求法，其中画出满足条件的几何体，并利用图形的直观性，帮助分析数量关系，是解答本题的关键．