
(本题满分14分)已知圆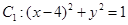 ,圆
,圆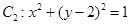 ,动点
,动点 到圆
到圆 ,
,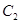 上点的距离的最小值相等.
上点的距离的最小值相等.
(1)求点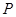 的轨迹方程;
的轨迹方程;
(2)点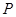 的轨迹上是否存在点
的轨迹上是否存在点 ,使得点
,使得点 到点
到点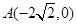 的距离减去点
的距离减去点 到点
到点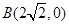 的距离的差为
的距离的差为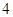 ,如果存在求出
,如果存在求出 点坐标,如果不存在说明理由.
点坐标,如果不存在说明理由.
(1)点 的轨迹方程是
的轨迹方程是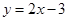 .(2)点
.(2)点 的轨迹上不存在满足条件的点
的轨迹上不存在满足条件的点 .
.
【解析】本试题主要是考查了动点的轨迹方程的求解,以及满足动点到定点的距离差为定值的点是否存在的探索性问题的运用。
((1)根据已知设出点的坐标,因为点到圆上点的距离的最小值相等,所以可知点到圆心的距离相等,因此得到轨迹方程。
(2)假设存在点满足题意可知,得到关于x,y的方程,然后利用方程有无解来判定是否存在的问题。
解:(1)设动点 的坐标为
的坐标为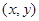 ,
,
圆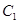 的圆心
的圆心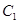 坐标为
坐标为 ,圆
,圆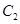 的圆心
的圆心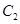 坐标为
坐标为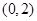 ,
,
因为动点 到圆
到圆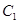 ,
,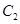 上的点距离最小值相等,所以
上的点距离最小值相等,所以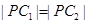 ,
,
即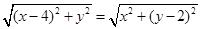 ,化简得
,化简得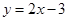 ,
,
因此点 的轨迹方程是
的轨迹方程是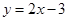 .
.
(2)假设这样的 点存在,设点
点存在,设点
因为 点到
点到 点的距离减去
点的距离减去 点到
点到 点的距离的差为4,
点的距离的差为4,
所以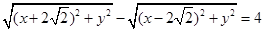 ,
,
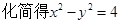 ,
,
又 点在直线
点在直线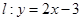 上,
上,  点的坐标是方程组
点的坐标是方程组 的解,
的解,
消元得 ,
,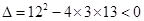 ,方程组无解,
,方程组无解,
所以点 的轨迹上不存在满足条件的点
的轨迹上不存在满足条件的点 .
.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源:2012-2013学年吉林省高三第一次月考文科数学试卷(解析版) 题型:解答题
(本题满分14分)已知函数
(1)若 ,求x的值;
,求x的值;
(2)若 对于
对于 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省惠州市高三第三次调研考试数学理卷 题型:解答题
(本题满分14分)
已知椭圆 :
: 的离心率为
的离心率为 ,过坐标原点
,过坐标原点 且斜率为
且斜率为 的直线
的直线 与
与 相交于
相交于 、
、 ,
, .
.
⑴求 、
、 的值;
的值;
⑵若动圆 与椭圆
与椭圆 和直线
和直线 都没有公共点,试求
都没有公共点,试求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省惠州市高三第三次调研考试数学理卷 题型:解答题
((本题满分14分)
已知梯形ABCD中,AD∥BC,∠ABC =∠BAD = ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图).
(1)当x=2时,求证:BD⊥EG ;
(2)若以F、B、C、D为顶点的三棱锥的体积记为 ,
,
求 的最大值;
的最大值;


(3)当 取得最大值时,求二面角D-BF-C的余弦值.
取得最大值时,求二面角D-BF-C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com