练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若=a+b,=a-b.

    ①当a、b满足什么条件时,a+b与a-b垂直?

    ②当a、b满足什么条件时,|a+b|=|a-b|?

    ③当a、b满足什么条件时,a+b平分a与b所夹的角?

    ④a+b与a-b可能是相等向量吗？

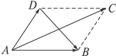
    图7

    解析:如图7,用向量构建平行四边形,其中向量、恰为平行四边形的对角线.

    由平行四边形法则,得

    =a+b,=-=a-b.

    由此问题就可转换为:

    ①当边AB、AD满足什么条件时,对角线互相垂直？(|a|=|b|)

    ②当边AB、AD满足什么条件时,对角线相等？(a、b互相垂直)

    ③当边AB、AD满足什么条件时,对角线平分内角？(a、b相等)

    ④a+b与B-b可能是相等向量吗？(不可能,因为对角线方向不同)

    点评:灵活的构想,独特巧妙,数形结合思想得到充分体现.由此我们可以想到在解决向量问题时,可以利用向量的几何意义构造几何图形,转化为平面几何问题,这就是数形结合解题的威力与魅力,教师引导学生注意领悟.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    若a＜b＜0，则下列结论不正确的是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列命题正确的是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    关于平面向量
    a
    ，
    b
    ，
    c
    ．有下列三个命题：
    ①若
    a
    •
    b
    =
    a
    •
    c
    ，则
    b
    =
    c
    ；
    ②若
    a
    =(1，k)，
    b
    =(-2，6)    ，
    a
    ∥
    b
    ，则k=-3；
    ③非零向量
    a
    和
    b
    满足|
    a
    |=|
    b
    |=|
    a
    -
    b
    |，则
    a
    与
    a
    +
    b
    的夹角为30°．
    其中真命题的序号为
    ②③
    ②③
    ．（写出所有真命题的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列四个结论中，正确的是
    （1），（3），（5）
    （1），（3），（5）

    （1）若A是B的必要不充分条件，则非B也是非A的必要不充分条件．
    （2）已知a，b∈R，则“|a+b|=|a|+|b|”的充要条件为“ab＞0”
    （3）
    a＞0
    △=b2-4ac≤0
    是“一元二次不等式ax2+bx+c≥0的解集为R的充要条件．”
    （4）“x≠1”是“x2≠1”的充分不必要条件．
    （5）“x≠0”是“x+|x|＞0”的必要不充分条件．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列四个命题：①若
    a
    •
    b
    =
    a
    •
    c
    ，则
    b
    =
    c
    ； ②若△ABC不是直角三角形，则tanAtanBtanC=tanA+tanB+tanC；③函数y=|tan
    x
    2
    |    的最小正周期为2π；④(
    a
    |
    a
    |
    +
    b
    |
    b
    |
    )•(
    .
    a
    |
    a
    |
    -
    b
    |
    b
    |
    )=0    ．其中正确的命题为
    ②③④
    ②③④
    ．（写出所有正确命题的序号）

    查看答案和解析>>

    同步练习册答案