解:(1)依题意得F
2(1,0),所以c=1,又过点(0,

),
因此a
2=b
2+c
2=4.
故所求的椭圆C
1的方程为:

,
2)
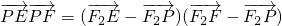
=
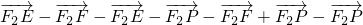
=
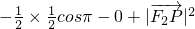
-
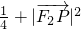
,
∵
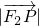
∈[1,3],∴

的最大值为
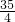
,
(3)由(1)知F
1(-1,0)以MN为直径的圆过F
1?
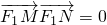
,
①若直线l斜率不存在.易知N(1,

),M(1,-

)
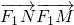
=
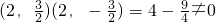
合题意,
若直线l斜率k存在,可设直线为y=k(x-1),M(x
1,y
1),N(x
2,y
2)
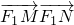
=(x
1+1,y
1)•(x
2+1,y
2)=(x
1+1)(x
2+1)+y
1y
2,
=(1+k
2)x
1x
2+(1-k
2)(x
1+x
2)+1+k
2 (*)
由

,知(3+4k
2)x
2-8k
2x+4k
2-12=0,
∴

,

,代入(*),
得
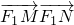
=
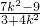
,
由
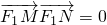
,得k=

,
所以存在满足条件的直线,方程为:

.
分析:(1)依题意得c=1,a
2=b
2+c
2=4.由此可求出椭圆C
1的方程.
2)
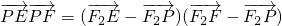
=
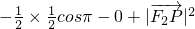
-
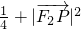
,由此可求出

的最大值.
(3)由题意知F
1(-1,0)以MN为直径的圆过F
1?
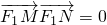
,设直线为y=k(x-1),M(x
1,y
1),N(x
2,y
2),
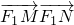
=(x
1+1,y
1)•(x
2+1,y
2)=(x
1+1)(x
2+1)+y
1y
2=(1+k
2)x
1x
2+(1-k
2)(x
1+x
2)+1+k
2,由

,知(3+4k
2)x
2-8k
2x+4k
2-12=0,再由根与系数的关系进行求解.
点评:本题考查圆锥曲线的性质和综合应用,难度较大,解题时要注意挖掘隐含条件,认真审题,利用根与系数的关系,仔细解答.

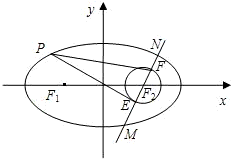 椭圆C1的中心在原点,过点(0,
椭圆C1的中心在原点,过点(0, ),且右焦点F2与圆C2:(x-1)2+y2=
),且右焦点F2与圆C2:(x-1)2+y2= 的圆心重合.
的圆心重合.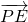
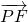 的最大值.
的最大值. ),
), ,
,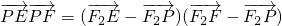
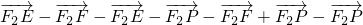
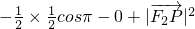 -
-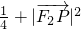 ,
,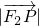 ∈[1,3],∴
∈[1,3],∴ 的最大值为
的最大值为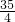 ,
,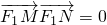 ,
, ),M(1,-
),M(1,- )
)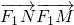 =
=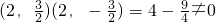 合题意,
合题意,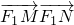 =(x1+1,y1)•(x2+1,y2)=(x1+1)(x2+1)+y1y2,
=(x1+1,y1)•(x2+1,y2)=(x1+1)(x2+1)+y1y2, ,知(3+4k2)x2-8k2x+4k2-12=0,
,知(3+4k2)x2-8k2x+4k2-12=0, ,
, ,代入(*),
,代入(*),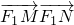 =
=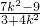 ,
,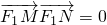 ,得k=
,得k= ,
, .
.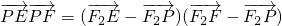 =
=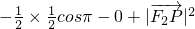 -
-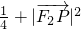 ,由此可求出
,由此可求出 的最大值.
的最大值.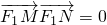 ,设直线为y=k(x-1),M(x1,y1),N(x2,y2),
,设直线为y=k(x-1),M(x1,y1),N(x2,y2),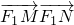 =(x1+1,y1)•(x2+1,y2)=(x1+1)(x2+1)+y1y2=(1+k2)x1x2+(1-k2)(x1+x2)+1+k2,由
=(x1+1,y1)•(x2+1,y2)=(x1+1)(x2+1)+y1y2=(1+k2)x1x2+(1-k2)(x1+x2)+1+k2,由 ,知(3+4k2)x2-8k2x+4k2-12=0,再由根与系数的关系进行求解.
,知(3+4k2)x2-8k2x+4k2-12=0,再由根与系数的关系进行求解.

 智慧小复习系列答案
智慧小复习系列答案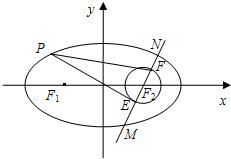 椭圆C1的中心在原点,过点(0,
椭圆C1的中心在原点,过点(0, (2005•海淀区二模)设椭圆C1的中心在原点,其右焦点与抛物线C2:y2=4x的焦点F重合,过点F与x轴垂直的直线与C1交于A、B两点,与C2交于C、D两点,已知
(2005•海淀区二模)设椭圆C1的中心在原点,其右焦点与抛物线C2:y2=4x的焦点F重合,过点F与x轴垂直的直线与C1交于A、B两点,与C2交于C、D两点,已知