试利用随机模拟方法计算曲线y=2x,x轴及x=±1所围成的“曲边梯形”的面积.
【答案】
分析:用随机模拟方法计算曲线y=2
x,x轴及x=±1所围成的“曲边梯形”的面积,分成四个步骤:
(1)利用计算机分别产生[-1,1]和[0,2]上的均匀随机数;
(2)统计试验总次数N和落在“曲边梯形”内的点数N
1(满足b<2
a的点(a,b)数).
(3)计算频率
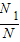
,得点落在“曲边梯形”上的概率近似值.(4)由几何概型得出“曲边梯形”面积的近似值.
解答:解:(1)利用计算机分别产生[-1,1]和[0,2]上的均匀随机数:a=-1+2Rand和b=2Rand,得随机数组(a,b).
(2)统计试验总次数N和落在“曲边梯形”内的点数N
1(满足b<2
a的点(a,b)数).
(3)计算频率
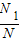
,得点落在“曲边梯形”上的概率近似值.
(4)由几何概型得p=
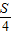
,所以
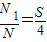
,于是得到S=
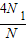
,这就是“曲边梯形”面积的近似值.
点评:本题考查模拟方法估计概率,考查几何概型,是一个比较好的题目,希望引起同学们重视.古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积和体积的比值得到.

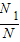 ,得点落在“曲边梯形”上的概率近似值.(4)由几何概型得出“曲边梯形”面积的近似值.
,得点落在“曲边梯形”上的概率近似值.(4)由几何概型得出“曲边梯形”面积的近似值.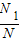 ,得点落在“曲边梯形”上的概率近似值.
,得点落在“曲边梯形”上的概率近似值.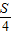 ,所以
,所以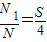 ,于是得到S=
,于是得到S=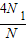 ,这就是“曲边梯形”面积的近似值.
,这就是“曲边梯形”面积的近似值.

 阅读快车系列答案
阅读快车系列答案